Next: Exercise 2 Up: Exercise 1 Previous: Statement
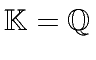 and
and
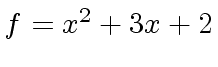 , compute a quasi-inverse of
, compute a quasi-inverse of
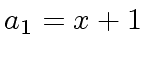 and
and
 .
.
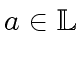 , with
, with 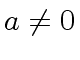 ,
possesses a quasi-inverse.
,
possesses a quasi-inverse.
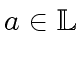 , with
, with 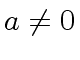 ,
can be computed in
,
can be computed in  operations in
operations in
A quasi-inverse of
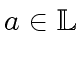 , with
, with 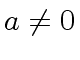 ,
tells us whether
,
tells us whether ![]() is invertible or a zero-divisor.
In practice, the second case is inconvenient.
For instance, division by a zero-divisor is not uniquely defined.
This motivates the last questions of this exercise.
From now on, we denote by
is invertible or a zero-divisor.
In practice, the second case is inconvenient.
For instance, division by a zero-divisor is not uniquely defined.
This motivates the last questions of this exercise.
From now on, we denote by ![]() a non-zero polynomial
in
a non-zero polynomial
in
![$ {\mbox{${\mathbb{K}}$}}[x]$](img24.png) with degree less than
with degree less than ![]() .
.
![$ {\mbox{${\mathbb{K}}$}}[x]$](img24.png) , show that one
can compute polynomials
, show that one
can compute polynomials
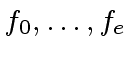 such that their product is
such that their product is
Analyzing the complexity for computing
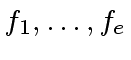 in question
in question ![]() is not easy and not required.
However, one special case is simpler: when
is not easy and not required.
However, one special case is simpler: when ![]() is squarefree,
that is, when for all non-constant polynomial
is squarefree,
that is, when for all non-constant polynomial
![$ h \in {\mbox{${\mathbb{K}}$}}[x]$](img30.png) ,
the polynomial
,
the polynomial ![]() does not divide
does not divide ![]() .
From now on, we assume that
.
From now on, we assume that ![]() is squarefree.
is squarefree.
![$ {\mbox{${\mathbb{K}}$}}[x]$](img24.png) , show that one
can compute polynomials
, show that one
can compute polynomials
![$ f_0, f_1 \in {\mbox{${\mathbb{K}}$}}[x]$](img33.png) such that
such that
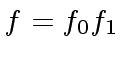 , and
, and
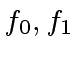 and the inverse of
and the inverse of  operations in
operations in
Marc Moreno Maza