Let
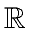 be a commutative ring and let
be a commutative ring and let 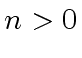 be a power of
be a power of 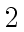 .
Let
.
Let 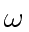 be a primitive
be a primitive 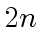 -th root of unity.
We consider the following polynomial
-th root of unity.
We consider the following polynomial
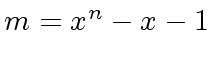 in
in
![$ {\mbox{${\mathbb{R}}$}}[x]$](img41.png) .
Let
.
Let
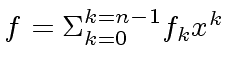 and
and
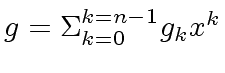 be two polynomials of degree less than
be two polynomials of degree less than 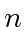 .
The goal of this exercise is to show that one can compute
.
The goal of this exercise is to show that one can compute
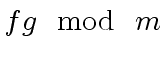 in
in
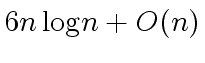 operations in
operations in
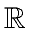 .
Let
.
Let 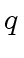 and
and 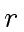 be the quotient and the remainder in the
division of
be the quotient and the remainder in the
division of 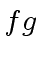 by
by 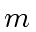 .
We define the polynomial
.
We define the polynomial
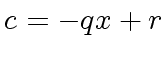 .
.
Marc Moreno Maza
2008-03-18
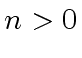 be a power of
be a power of 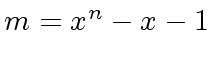 in
in
![$ {\mbox{${\mathbb{R}}$}}[x]$](img41.png) .
Let
.
Let
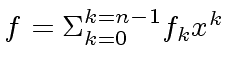 and
and
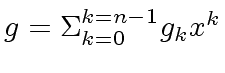 be two polynomials of degree less than
be two polynomials of degree less than 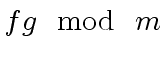 in
in
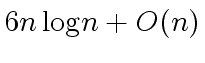 operations in
operations in
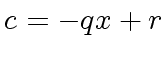 .
.