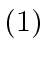
- Show that
 can be computed in
can be computed in
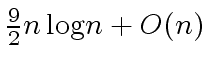 operations in
operations in
 .
.

- Reusing the results of the intermediate calculations of
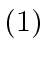 ,
show that no more than
,
show that no more than
 operations in
operations in
 are needed for computing
are needed for computing 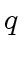 .
.

- Deduce that
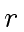 can be computed in
can be computed in
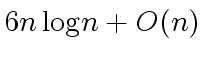 operations in
operations in
 .
.
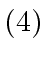
- Give a sharp estimate for the naive approach, that is
for:
- computing the product
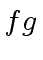 in
in
![$ {\mbox{${\mathbb{R}}$}}[x]$](img41.png) and then
and then
- computing the division of
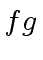 by
by  .
.
Marc Moreno Maza
2008-03-18
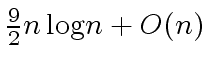 operations in
operations in
 operations in
operations in
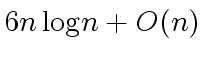 operations in
operations in
![$ {\mbox{${\mathbb{R}}$}}[x]$](img41.png) and then
and then