Next: Questions Up: Exercise 4 Previous: Exercise 4
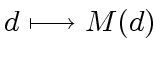 be a multiplication time.
Hence, for any two polynomials
be a multiplication time.
Hence, for any two polynomials
![$ f, g \in {\mbox{${\mathbb{R}}$}}[x]$](img56.png) of degree less than
of degree less than 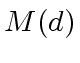 operations in
operations in
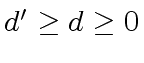 we have
we have
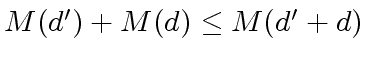 .
.
Let
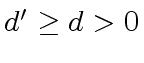 be two integers.
Let
be two integers.
Let
![$ f \in {\mbox{${\mathbb{R}}$}}[x]$](img62.png) be of degree
be of degree ![]() and let
and let
![$ m_1, \ldots, m_r \in {\mbox{${\mathbb{R}}$}}[x]$](img64.png) be monic polynomials
such that the sum of their degrees
be monic polynomials
such that the sum of their degrees
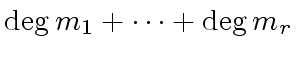 is
is ![]() .
.
The goal of this exercise is to show that all remainders
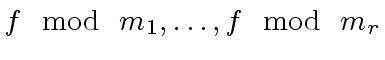 can be computed in
can be computed in
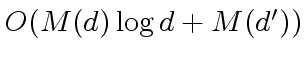 operations in
operations in
![]() .
.
The following result (to be proved in class) will be essential:
division-with-remainder of a polynomial
![$ a \in {\mbox{${\mathbb{R}}$}}[x]$](img68.png) of degree
of degree 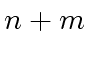 by a monic polynomial
by a monic polynomial
![$ b \in {\mbox{${\mathbb{R}}$}}[x]$](img70.png) of degree
of degree ![]() (where
(where 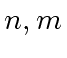 are non-negative integers)
can be done in at most
are non-negative integers)
can be done in at most 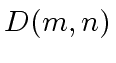 ring operations in
ring operations in
![]() where we have
where we have
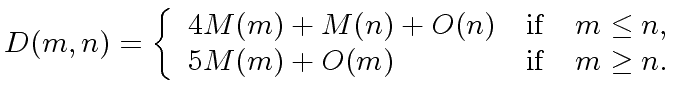 |
Marc Moreno Maza