Next: Bibliography Up: Exercise 4 Previous: Statement
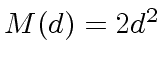 .
Compare the costs of the following two approaches:
.
Compare the costs of the following two approaches:
 and then, the remainders
and then, the remainders
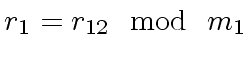 and
and
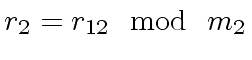 ,
,
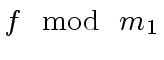 and
and
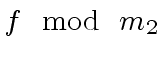 directly.
directly.
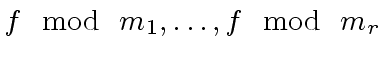 can be computed in
can be computed in
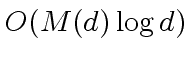 operations in
operations in
Marc Moreno Maza