Next: The complexity of divide-and-conquer algorithms Up: A review of complexity notions Previous: A review of complexity notions
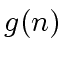 is in the ORDER OF MAGNITUDE
of
is in the ORDER OF MAGNITUDE
of 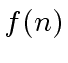 and we write
and we write
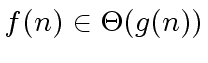 if
there exist two (strictly) positive constants
if
there exist two (strictly) positive constants 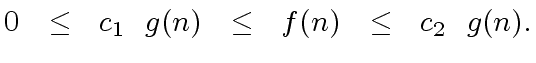 |
(2) |
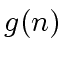 is an ASYMPTOTIC UPPER BOUND
of
is an ASYMPTOTIC UPPER BOUND
of 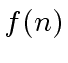 and we write
and we write
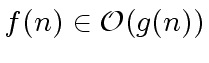 if there exists
a (strictly) positive constants
if there exists
a (strictly) positive constants  |
(3) |
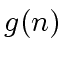 is an ASYMPTOTIC LOWER BOUND
of
is an ASYMPTOTIC LOWER BOUND
of 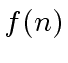 and we write
and we write
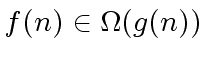 if there exists
a (strictly) positive constants
if there exists
a (strictly) positive constants  |
(4) |
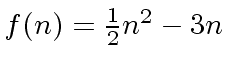 and
and
 we have
we have
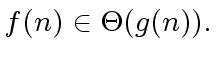 Indeed we have
Indeed we have
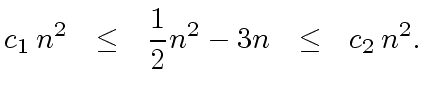 |
(5) |
 with
with
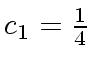 and
and
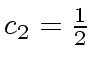 .
.
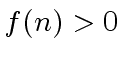 and
and 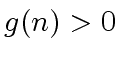 for every
for every
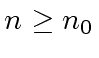 .
Then we have
.
Then we have
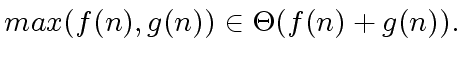 |
(6) |
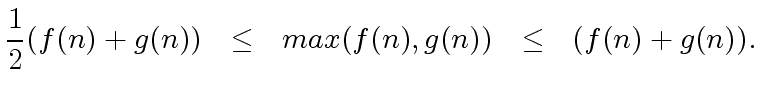 |
(7) |
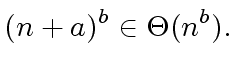 |
(8) |
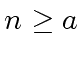 we have
we have
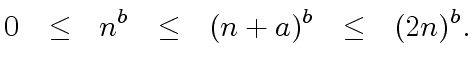 |
(9) |
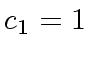 and
and
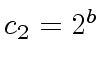 .
.
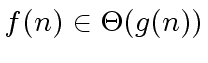 holds iff
holds iff
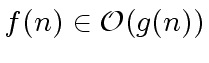 and
and
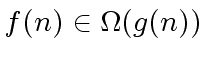 hold together.
hold together.
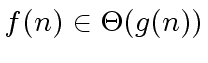 ,
,
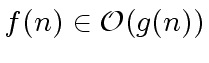 and
and
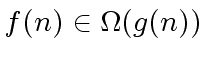 define a reflexive and transitive binary relation
among the
define a reflexive and transitive binary relation
among the
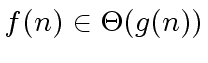 is symmetric.
is symmetric.
 |
(10) |
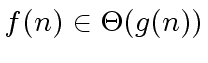 ,
,
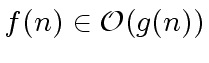 and
and
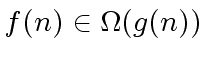 .
Hence, the following
.
Hence, the following
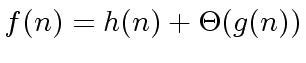 |
(11) |
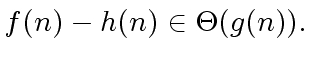 |
(12) |
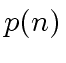 be a (univariate) polynomial with degree
be a (univariate) polynomial with degree 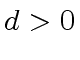 .
Let
.
Let 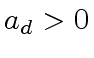 .
Then we have
.
Then we have
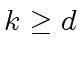 then
then
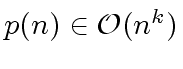 ,
,
 then
then
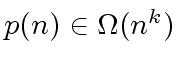 ,
,
 .
.
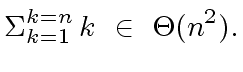 |
(13) |
Marc Moreno Maza