Next: Implementing Computer Algebra: basic ideas Up: A review of complexity notions Previous: Orders of magnitude
DIVIDE-AND-CONQUER ALGORITHMS proceed as follows.
EQUATION SATISFIED BY
![]() .
Let
.
Let 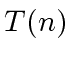 be the time complexity of a divide-and-conquer algorithm
to solve this problem.
Then
be the time complexity of a divide-and-conquer algorithm
to solve this problem.
Then 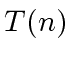 satisfies an equation of the form:
satisfies an equation of the form:
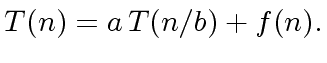 |
(14) |
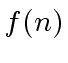 is the cost of the combine-part,
is the cost of the combine-part, 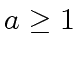 is the
number of recursively calls and
is the
number of recursively calls and 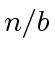 with
with 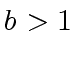 is the size of a sub-problem.
is the size of a sub-problem.
LABELED TREE ASSOCIATED WITH THE EQUATION.
Assume ![]() is a power of
is a power of ![]() , say
, say ![]() To solve this equation we can associate a labeled tree
To solve this equation we can associate a labeled tree
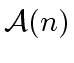 to it
as follows.
to it
as follows.
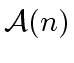 is reduced to a single leaf by labeled
is reduced to a single leaf by labeled 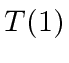 .
.
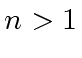 , then the root of
, then the root of
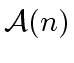 is labeled
by
is labeled
by 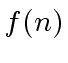 and
and
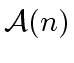 possesses
possesses
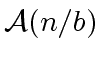 .
.
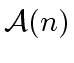 associated with
associated with
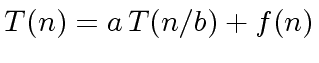 has height
has height 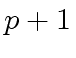 .
Moreover the sum of its labels is
.
Moreover the sum of its labels is 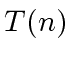 .
.
LET US GIVE TWO EXAMPLES.
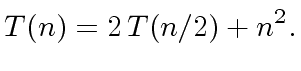 |
(15) |
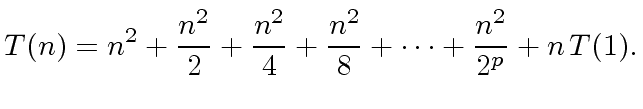 |
(16) |
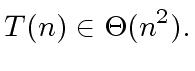 |
(17) |
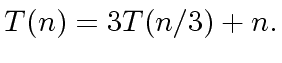 |
(18) |
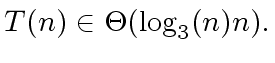 |
(19) |
A FORMULA TO ESTIMATE
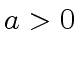 be an integer and let
be an integer and let
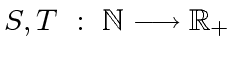 be functions
such that
be functions
such that
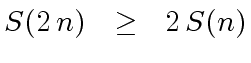 and
and
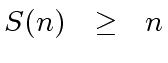 .
.
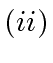
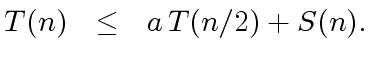
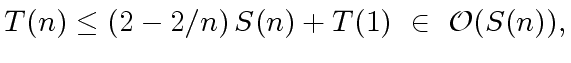 |
(20) |
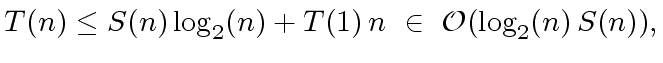 |
(21) |
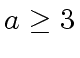 then
then
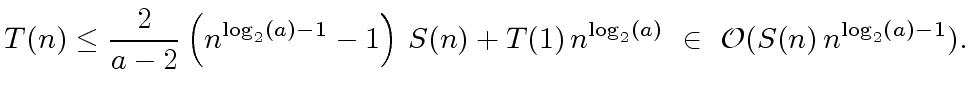 |
(22) |
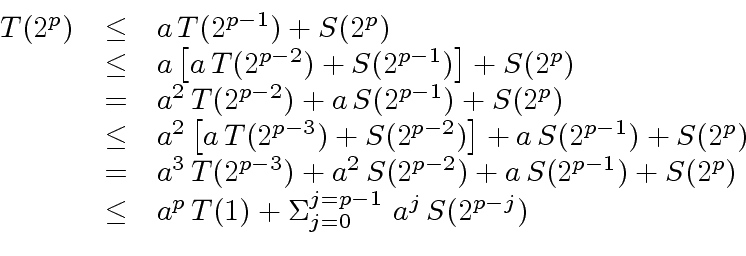 |
(23) |
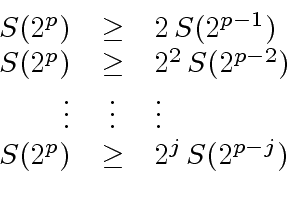 |
(24) |
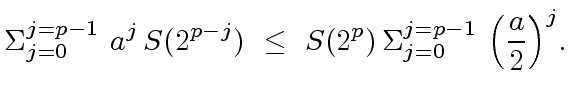 |
(25) |
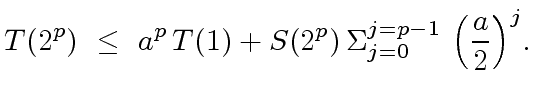 |
(26) |
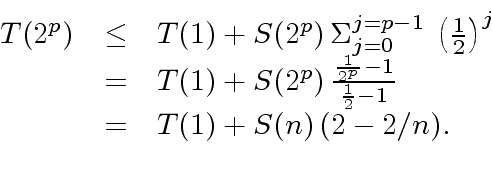 |
(27) |
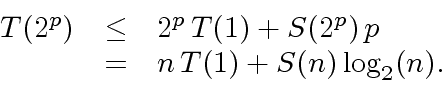 |
(28) |
Marc Moreno Maza