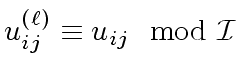Proof.
Let
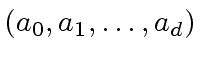
be a
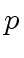
-adic expansion of
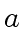
w.r.t.
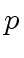
.
Let
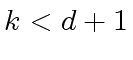
be a positive integer.
By Proposition
6,
the element
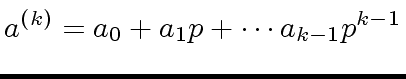 |
(12) |
is a
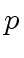
-adic approximation of
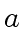
at order

.
By Proposition
4
there exists a polynomial
![$ {\psi} \in R[y]$](img83.png)
such that
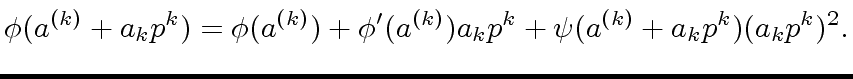 |
(13) |
Since we have
we deduce from Proposition
7
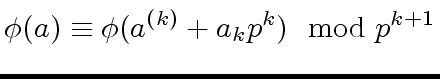 |
(14) |
Since
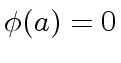
this shows that
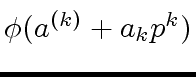
is in the ideal generated by
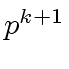
.
Similarly,
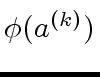
is in the ideal generated by

.
Therefore we can divide
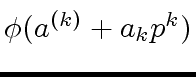
and
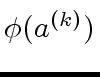
by

, leading to
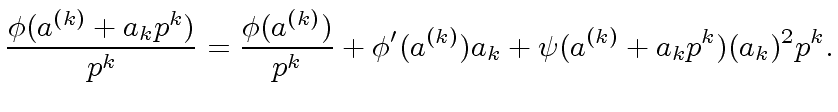 |
(15) |
Now observe that
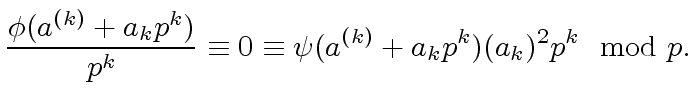 |
(16) |
Let us denote by
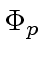
the canonical homomorphism from

to
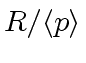
.
Then we obtain
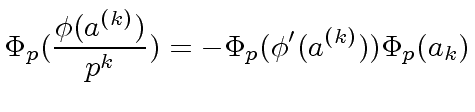 |
(17) |
Now, since

holds we have
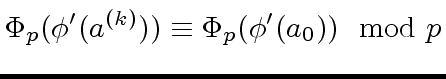 |
(18) |
Since
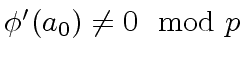
holds we can solve
Equatiion
17
for
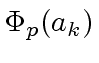
.
Finally, from Theorem
1,
we have
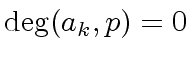
such that we can
view
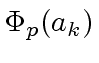
as
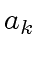
. This is straightforward if
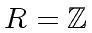
or if
![$ R = {\bf k}[x]$](img138.png)
where
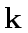
is a field, since we can choose for
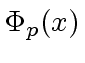
the remainder of
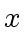
modulo
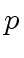
.

Proof.
We proceed by induction on
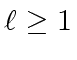
.
For
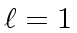
the claim follows from the hypothesis of the theorem.
So let
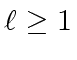
be such that the claim is true.
Hence there exist
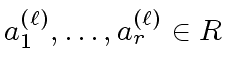
such that
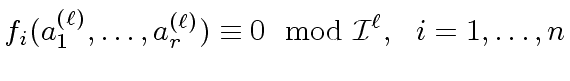 |
(20) |
and
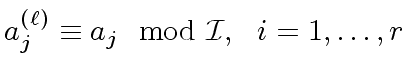 |
(21) |
Since
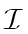
is finitely generated, then so is
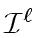
and let
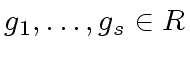
such that
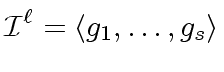 |
(22) |
Therefore, for every

, there exist

such that
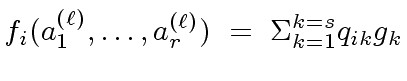 |
(23) |
For each
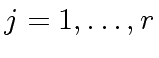
we want to compute
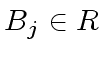
such that
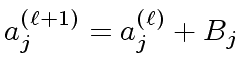 |
(24) |
is the desired
next approximation.
We impose
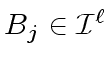
so let

be such that
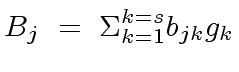 |
(25) |
Using Proposition
5
we obtain
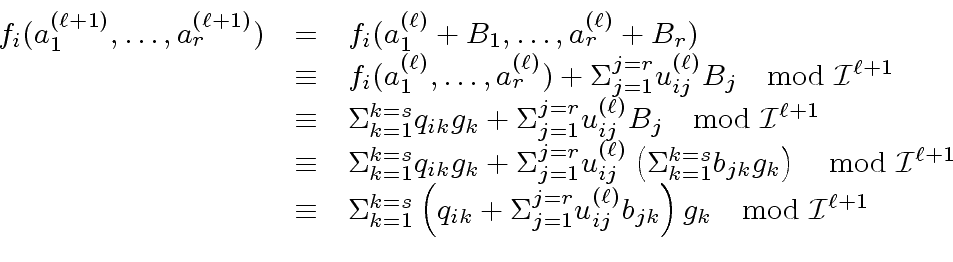 |
(26) |
where

is the Jacobian matrix
of
at
.
Hence, solving for
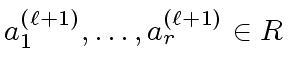 such that
such that
leads to solving the system of linear equations:
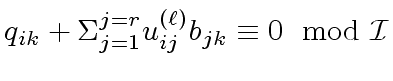 |
(27) |
for
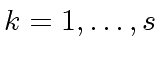
and
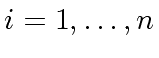
.
Now using
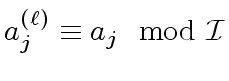 for
for
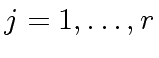 we obtain
we obtain
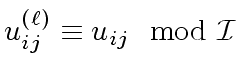 |
(28) |
Therefore the linear system equations
given by Relation (
27)
has solutions.

 be a prime element.
Let
be a prime element.
Let
![$ {\phi} \in R[y]$](img64.png) and let
and let
 such that
such that
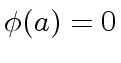 ,
,
 ,
,
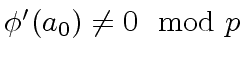 .
.
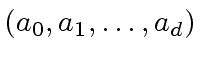 be a
be a 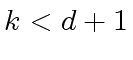 be a positive integer.
By Proposition 6,
the element
be a positive integer.
By Proposition 6,
the element
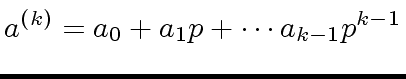
![$ {\psi} \in R[y]$](img83.png) such that
such that
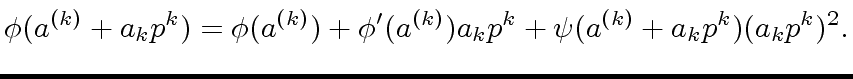
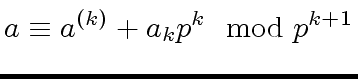
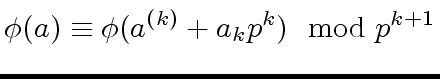
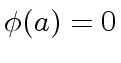 this shows that
this shows that
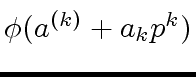 is in the ideal generated by
is in the ideal generated by 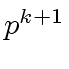 .
Similarly,
.
Similarly,
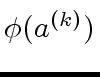 is in the ideal generated by
is in the ideal generated by 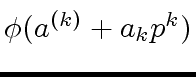 and
and
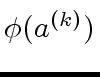 by
by 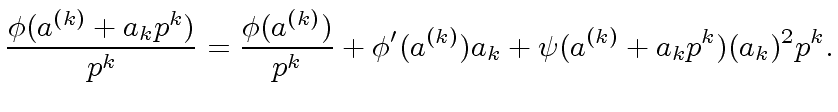
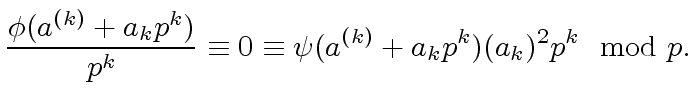
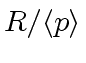 .
Then we obtain
.
Then we obtain
 holds we have
holds we have
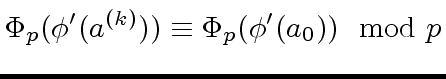
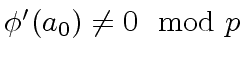 holds we can solve
Equatiion 17
for
holds we can solve
Equatiion 17
for
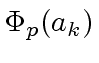 .
Finally, from Theorem 1,
we have
.
Finally, from Theorem 1,
we have
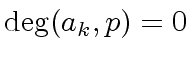 such that we can view
such that we can view
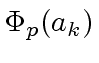 as
as ![$ R = {\bf k}[x]$](img138.png) where
where 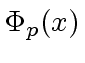 the remainder of
the remainder of ![$ f_1, \ldots, f_n \in R[x_1, \ldots, x_r]$](img141.png) be
be 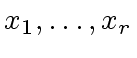 .
Let
.
Let
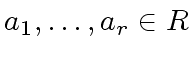 be elements.
Let
be elements.
Let 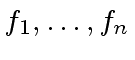 evaluated at
evaluated at
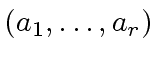 .
That is,
.
That is, 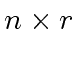 matrix defined by
matrix defined by
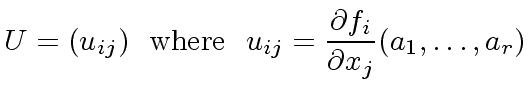
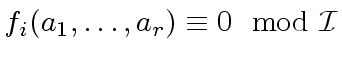 .
.
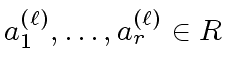 such that
such that
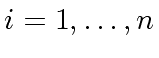 we have
we have
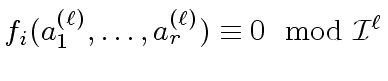 ,
,
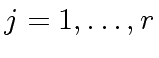 we have
we have
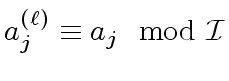 .
.
 .
For
.
For
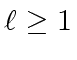 be such that the claim is true.
Hence there exist
be such that the claim is true.
Hence there exist
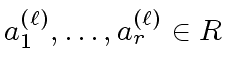 such that
such that
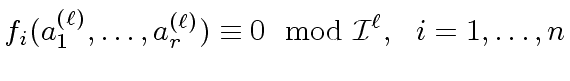
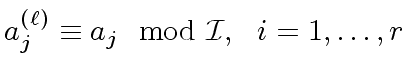
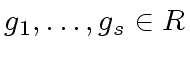 such that
such that
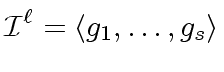
 , there exist
, there exist
 such that
such that
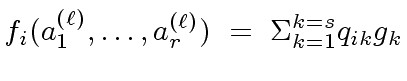
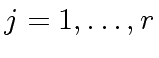 we want to compute
we want to compute 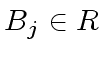 such that
such that
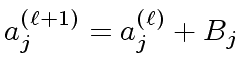
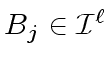 so let
so let
 be such that
be such that
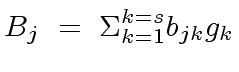
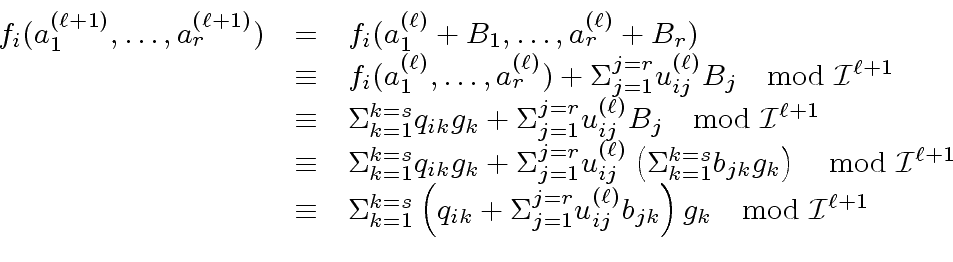
 is the Jacobian matrix
of
is the Jacobian matrix
of
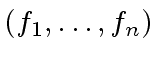 at
at
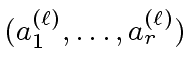 .
.
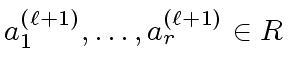 such that
such that
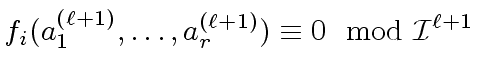
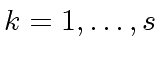 and
and
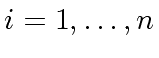 .
.
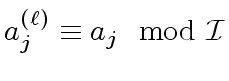 for
for
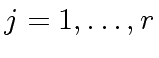 we obtain
we obtain