Next: A modular Gcd Algorithm in Up: Advanced Computer Algebra: The resultant Previous: Modular Gcd Algorithms in
![$ {\mbox{${\mathbb{Z}}$}}[x_1, \ldots, x_n]$](img111.png)
![$ {\mbox{${\mathbb{Z}}$}}/{\langle p \rangle}[x_1, \ldots, x_n]$](img375.png) .
Algorithm 4
computes the gcd of two polynomials
.
Algorithm 4
computes the gcd of two polynomials
![$ f,g \in {\mbox{${\mathbb{Z}}$}}[x_1, \ldots, x_n]$](img376.png) with this assumption.
Observe that Algorithm 4
takes as input any couple of multivariate polynomials over
with this assumption.
Observe that Algorithm 4
takes as input any couple of multivariate polynomials over
Algorithm 4 relies also on the following technical assumptions.
![$ f \in {\mbox{${\mathbb{Z}}$}}[x_1, \ldots, x_n] \ \longmapsto \ {\rm content}_{\mbox{${\mathbb{Z}}$}}(f)$](img377.png) computes the content of a multivariate polynomial over
computes the content of a multivariate polynomial over
![$ (f \in {\mbox{${\mathbb{Z}}$}}[x_1, \ldots, x_n], c \in R) \ \longmapsto \ f \ \mbox{{\sf exquo}} \ c$](img378.png) is
the exact division of a polynomial by an integer. That is, assuming
that
is
the exact division of a polynomial by an integer. That is, assuming
that 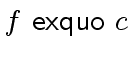 is the polynomial
is the polynomial
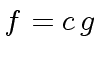 .
.
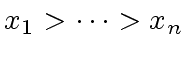 .
Then to order monomials we use the lexicographic ordering induced by
.
Then to order monomials we use the lexicographic ordering induced by
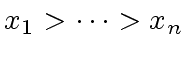 .
.
![$ f \in {\mbox{${\mathbb{Z}}$}}[x_1, \ldots, x_n] \ \longmapsto \ {\rm lc}_{lex}(f)$](img382.png) returns the leading coefficient of
returns the leading coefficient of 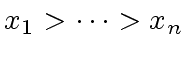 .
.
![$ f \in {\mbox{${\mathbb{Z}}$}}[x_1, \ldots, x_n] \ \longmapsto \ {\deg}_{lex}(f)$](img383.png) returns the degreeof
returns the degreeof 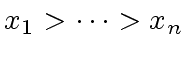 . That is the exponent vector
of the leading monomial of
. That is the exponent vector
of the leading monomial of
Observations.
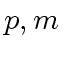 )(
)(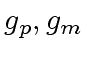 ) is in fact a series
of CRA: one per monomial. Remember the case of the
fast multication in
) is in fact a series
of CRA: one per monomial. Remember the case of the
fast multication in
![$ {\mbox{${\mathbb{Z}}$}}[x]$](img46.png) based on the FFT.
based on the FFT.
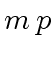 so that negative integer
coefficients in
so that negative integer
coefficients in 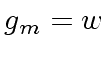 |
(115) |
Marc Moreno Maza