

Next: Efficient implementation
Up: Computing primitive n mathend000#-th roots
Previous: Primitive n mathend000#-th roots of
We explain in this section a simple probabilistic approach
for computing primitive n
mathend000#-roots of unity in
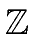 /p
/p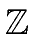 mathend000#.
Of course, we assume that n
mathend000# divides p - 1
mathend000#.
Hence, there exists an integer q
mathend000# such that
p = qn + 1
mathend000# holds.
According to little Fermat's theorem,
for all
mathend000#.
Of course, we assume that n
mathend000# divides p - 1
mathend000#.
Hence, there exists an integer q
mathend000# such that
p = qn + 1
mathend000# holds.
According to little Fermat's theorem,
for all
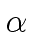
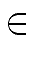
 mathend000#, with
mathend000#, with
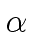
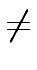 0
mathend000# and
0
mathend000# and
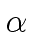
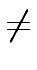 1
mathend000#, we have
1
mathend000#, we have
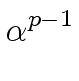 = 1. = 1. |
(53) |
Therefore, we obtain
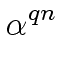 = 1. = 1. |
(54) |
It follows that
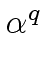 mathend000# is a candidate for being
a primitive n
mathend000#-th root of unity.
If
mathend000# is a candidate for being
a primitive n
mathend000#-th root of unity.
If
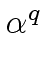 mathend000# is not a primitive n
mathend000#-root root of unity
then:
mathend000# is not a primitive n
mathend000#-root root of unity
then:
- the sequence of the
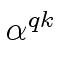 mathend000# for
k = 0,..., n - 1
mathend000# is periodic, with a period dividing n
mathend000#, and
mathend000# for
k = 0,..., n - 1
mathend000# is periodic, with a period dividing n
mathend000#, and
- in particular
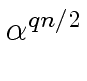 = 1
mathend000# holds.
= 1
mathend000# holds.
Since
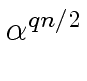 mathend000# equals either 1
mathend000# or -1
mathend000#, we have the following.
mathend000# equals either 1
mathend000# or -1
mathend000#, we have the following.
Proposition 5
Let p > 2
mathend000# be a prime number and let n, q
mathend000# be integers such that n
mathend000# is a power of 2
such that we have
p = nq + 1
mathend000#.
Let
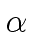
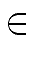
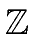 /p
/p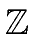 mathend000# different from 0
mathend000# and 1
mathend000#.
Then,
mathend000# different from 0
mathend000# and 1
mathend000#.
Then,
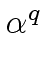 mathend000# is a primitive n
mathend000#-th root of unity
if and only if
mathend000# is a primitive n
mathend000#-th root of unity
if and only if
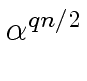 = - 1
mathend000# holds.
= - 1
mathend000# holds.
This proposition is very easy to implement and provides
an efficient way to compute primitive roots of unity in practice.
It avoids the construction of tables of primitive roots of unity,
which was a usual approach as detailed above.


Next: Efficient implementation
Up: Computing primitive n mathend000#-th roots
Previous: Primitive n mathend000#-th roots of
Marc Moreno Maza
2007-01-10
![]() /p
/p![]()
![]()
![]()
![]()
![]()
![]() 0
0
![]()
![]() 1
1
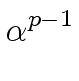 = 1.
= 1.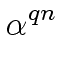 = 1.
= 1.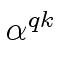
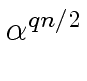 = 1
= 1
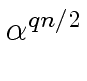
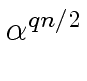 = - 1
= - 1