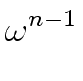 } } |
(42) |
Conversly, it is known from finite field theory that Gp-1
![]()
Gp-1 = {1,
![]() ,
,![]() ,...,
,...,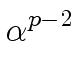 }
}
(43)
Recall that
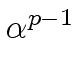 = 1
= 1
Then we have
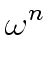 = 1.
= 1.
(45)
For all 0 < k < n
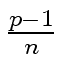 < p - 1
< p - 1
![]() =
= 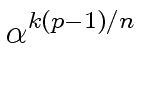
![]() 1.
1.
(46)
This shows that ![]()
![]()
We could use brute force. Given
![]() /p
/p![]()
![]() Gp-1
Gp-1
However we can reduce the complexity of this search by
computing a generator of Gp-1
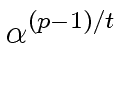 |
(47) |
1 < n < p - 1 and 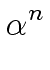 = 1. = 1. |
(48) |
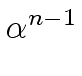 }
}
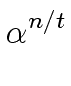 . . |
(49) |
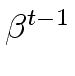 }
}
| p = q 2k + 1 | (50) |
But not all numbers of the form
q 2k + 1
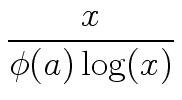 |
(51) |
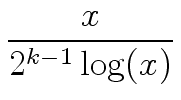 |
(52) |
Let
x = 231
In the BasicMath library, one of the parents of libalgebra, nice primes are organized in tables. So there is a category for tables of primes!
macro SI == SingleInteger;
PrimesTableCategory(s: SI): Category == with {
sizeBound: () -> SI;
tableSize: () -> SI;
rank: SI -> Partial(SI);
maxPrime: () -> SI;
minPrime: () -> SI;
previousPrime: SI -> SI;
nextPrime: SI -> SI;
primes: () -> Generator(SI);
FourierDegree: SI -> SI;
getPrimeOfFourierDegree: SI -> SI;
nextPrimeOfFourierDegree: (SI, SI) -> SI;
unitsGenerator: SI -> SI;
primitiveRootofUnity: (SI, SI) -> SI;
}
where
macro SI == SingleInteger;
FourierPrimesTableCategory(r: SI, s: SI): Category == with {
FourierDegree: () -> SI
sizeBound: () -> SI
tableSize: () -> SI
rank: SI -> Partial(SI)
maxPrime: () -> SI
minPrime: () -> SI
previousPrime: SI -> SI
nextPrime: SI -> SI
primes: () -> Generator(SI)
unitsGenerator: SI -> SI
primitiveRootofUnity: (SI, SI) -> SI
}
whereFourierPrimesTableCategory(r,s) specifies the operations that
we expect from the table of Fourier primes p
F6P15: FourierPrimesTableCategory(6,15) == add {
local fd: SI == 6;
local sb: SI == 15;
--------------------------------------------------------------------
-- Table (6,15) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^6
-- Number of 6-Fourier primes less than 2^15 is 58
MAXINDEX: SingleInteger == 58;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[193, 449, 577, 1217, 1601, 2113, 2753, 3137,
4289, 4673, 4801, 5441, 5569, 5953, 6337, 6977,
7489, 7873, 8513, 8641, 9281, 10177, 10433, 11329,
11969, 12097, 13121, 13249, 13633, 14401, 14657, 15809,
15937, 16193, 17729, 19009, 19777, 20161, 20929, 21313,
21569, 22721, 23873, 24001, 25153, 25409, 25537, 25793,
26177, 26561, 27073, 27329, 27457, 28097, 29633, 29761,
30529, 32321];
-- The corresponding units generators are:
local generatorList: Array SingleInteger :=
[5, 3, 5, 3, 3, 5, 3, 3,
3, 3, 7, 3, 13, 7, 10, 3,
7, 5, 5, 17, 3, 7, 3, 7,
3, 5, 7, 7, 5, 11, 3, 3,
7, 5, 3, 23, 11, 13, 7, 5,
3, 3, 3, 14, 10, 3, 10, 3,
3, 3, 5, 3, 7, 3, 3, 17,
13, 6];
FourierDegree(): SI == fd;
sizeBound(): SI == sb;
tableSize(): SI == MAXINDEX;
..............................................
}
F7P15: FourierPrimesTableCategory(7,15) == add {
local fd: SI == 7;
local sb: SI == 15;
--------------------------------------------------------------------
-- Table (7,15) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^7
-- Number of 7-Fourier primes less than 2^15 is 29
MAXINDEX: SingleInteger == 29;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[641, 1153, 1409, 2689, 3457, 4481, 4993, 6529,
7297, 9601, 9857, 10369, 11393, 12161, 13441, 13697,
15233, 16001, 18049, 19073, 19841, 20353, 21121, 21377,
26497, 28289, 29569, 30593, 31873];
-- The corresponding units generators are:
local generatorList: Array SingleInteger :=
[3, 5, 3, 19, 7, 3, 5, 7,
5, 13, 5, 13, 3, 3, 11, 3,
3, 3, 13, 3, 3, 5, 19, 3,
5, 6, 17, 3, 11];
FourierDegree(): SI == fd;
sizeBound(): SI == sb;
tableSize(): SI == MAXINDEX;
...........................................................
F8P15: FourierPrimesTableCategory(8,15) == add {
local fd: SI == 8;
local sb: SI == 15;
--------------------------------------------------------------------
-- Table (8,15) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^8
-- Number of 8-Fourier primes less than 2^15 is 12
MAXINDEX: SingleInteger == 12;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[257, 769, 3329, 7937, 9473, 14081, 14593, 22273,
23297, 26881, 30977, 31489];
-- The corresponding units generators are:
local generatorList: Array SingleInteger :=
[3, 11, 3, 3, 3, 3, 5, 5,
3, 11, 3, 7];
FourierDegree(): SI == fd;
sizeBound(): SI == sb;
tableSize(): SI == MAXINDEX;
...........................................................
9P23: FourierPrimesTableCategory(9,23) == add {
local fd: SI == 9;
local sb: SI == 23;
--------------------------------------------------------------------
-- Table (9,23) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^9
-- Number of 9-Fourier primes less than 2^23 is 1092
MAXINDEX: SingleInteger == 1092;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[7681, 10753, 11777, 17921, 23041, 26113, 32257,
...........................................................
F10P24: FourierPrimesTableCategory(10,24) == add {
local fd: SI == 10;
local sb: SI == 24;
--------------------------------------------------------------------
-- Table (10,24) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^10
-- Number of 10-Fourier primes less than 2^24 is 1087
MAXINDEX: SingleInteger == 1087;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[13313, 15361, 19457, 25601,
...........................................................
F11P25: FourierPrimesTableCategory(11,25) == add {
local fd: SI == 11;
local sb: SI == 25;
--------------------------------------------------------------------
-- Table (11,25) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^11
-- Number of 11-Fourier primes less than 2^25 is 978
MAXINDEX: SingleInteger == 978;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[18433,
...........................................................
F12P26: FourierPrimesTableCategory(12,26) == add {
local fd: SI == 12;
local sb: SI == 26;
--------------------------------------------------------------------
-- Table (12,26) --
--------------------------------------------------------------------
-- Maximal size for a FFT: 2^12
-- Number of 12-Fourier primes less than 2^26 is 972
MAXINDEX: SingleInteger == 972;
-- These Fourier primes are:
local primeList: Array SingleInteger :=
[12289,
...........................................................