

Next: Computing primitive n mathend000#-th roots
Up: Fast Polynomial Multiplication based on
Previous: The Fast Fourier Transform
Algorithm 2
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $f,g \in ...
...amma}) \ = \ 1/n \, DTF_{{\omega}^{-1}}({\gamma})$
\end{tabbing}\end{minipage}}](img92.png) mathend000#
mathend000#
Theorem 2
Let n
mathend000# be a power of 2
mathend000# and
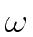
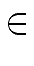 R
mathend000# a primitive n
mathend000#-th
root of unity.
Then convolution in
R[x]/
R
mathend000# a primitive n
mathend000#-th
root of unity.
Then convolution in
R[x]/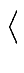 xn-1
xn-1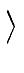 mathend000# and
multiplication in R[x]
mathend000# of polynomials whose product has degree less than n
mathend000#
can be performed using
mathend000# and
multiplication in R[x]
mathend000# of polynomials whose product has degree less than n
mathend000#
can be performed using
-
3 n log(n)
mathend000# additions in R
mathend000#,
-
3/2 n log(n) + n - 2
mathend000# multiplications by a power of
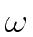 mathend000#,
mathend000#,
- n
mathend000# multiplications in R
mathend000#,
- n
mathend000# divisions by n
mathend000# (as an element of R
mathend000#),
leading to
9/2 n log(n) + 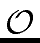 (n)
mathend000# operations in R
mathend000#.
(n)
mathend000# operations in R
mathend000#.
Figure:
FFT-based univariate polynomial multiplication over
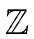 /p
/p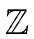 mathend000#
mathend000#
![\begin{figure}\htmlimage[no_transparent]
\centering
\includegraphics[scale=0.5]{fftflowchart.eps}
\end{figure}](img93.png) |


Next: Computing primitive n mathend000#-th roots
Up: Fast Polynomial Multiplication based on
Previous: The Fast Fourier Transform
Marc Moreno Maza
2007-01-10
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $f,g \in ...
...amma}) \ = \ 1/n \, DTF_{{\omega}^{-1}}({\gamma})$
\end{tabbing}\end{minipage}}](img92.png)