

Next: Primitive roots of unity
Up: Foundations of Computer Algebra: Fast
Previous: Foundations of Computer Algebra: Fast
In the whole section we consider a commutative ring R
mathend000# with units.
Let us consider two univariate polynomials
f, g 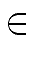 R[x]
mathend000#
of degree less than n
mathend000#. Then their product has degree less than 2n - 1
mathend000#.
Assume that we are given a finite subset
P
mathend000# of R
mathend000# with
2 n - 1
mathend000# elements such that
f (r)
mathend000# and g(r)
mathend000# are known for every r
R[x]
mathend000#
of degree less than n
mathend000#. Then their product has degree less than 2n - 1
mathend000#.
Assume that we are given a finite subset
P
mathend000# of R
mathend000# with
2 n - 1
mathend000# elements such that
f (r)
mathend000# and g(r)
mathend000# are known for every r 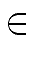 R
mathend000#.
Then the values
f (r) g(r)
mathend000# define the polynomial f g
mathend000# completely.
Indeed, by Lagrange interpolation we construct the polynomial
f g
mathend000# (which has at most 2n - 1
mathend000# coefficients) from the
2 n - 1
mathend000# values
f (r) g(r)
mathend000#.
Observe that the cost of defining f g
mathend000# by the values
f (r) g(r)
mathend000#
is 2 n - 1
mathend000#, which is cheap!
R
mathend000#.
Then the values
f (r) g(r)
mathend000# define the polynomial f g
mathend000# completely.
Indeed, by Lagrange interpolation we construct the polynomial
f g
mathend000# (which has at most 2n - 1
mathend000# coefficients) from the
2 n - 1
mathend000# values
f (r) g(r)
mathend000#.
Observe that the cost of defining f g
mathend000# by the values
f (r) g(r)
mathend000#
is 2 n - 1
mathend000#, which is cheap!
However if we need information about f g
mathend000# such as its
leading coefficient or its number of terms we need to
compute the coefficients of f g
mathend000#.
The cost of this construction is in
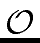 (n2)
mathend000#.
(n2)
mathend000#.
The underlying idea of the fast polynomial multiplication based
on the discrete Fourier transform is the following.
Assume that there exists a subset P
mathend000# of R
mathend000# with
2 n - 1
mathend000# elements such that
- evaluating f
mathend000# and g
mathend000# at every r
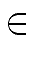 P
mathend000# can be done
at nearly linear time cost (such as
P
mathend000# can be done
at nearly linear time cost (such as
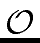 (n log(n))
mathend000#),
(n log(n))
mathend000#),
- interpolating
f (r) g(r)
mathend000# for r
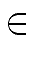 P
mathend000# can be done
at nearly linear time cost.
P
mathend000# can be done
at nearly linear time cost.
Then the multiplication of f
mathend000# by g
mathend000#, represented by their
coefficients, can be done in
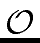 (n log(n))
mathend000#.
(n log(n))
mathend000#.
Such sets P
mathend000# do not always exist. This depends on the ring R
mathend000#
and the degrees of the polynomials f
mathend000# and g
mathend000#.
However many finite fields possess such sets for small enough degrees
of f
mathend000# and g
mathend000#.
For the arbitrary ring R
mathend000#, it can be shown that the multiplication
of f
mathend000# nad g
mathend000#, represented by their
coefficients, can be done in
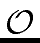 (n log(n)log(log(n)))
mathend000#.
(n log(n)log(log(n)))
mathend000#.
Subsections


Next: Primitive roots of unity
Up: Foundations of Computer Algebra: Fast
Previous: Foundations of Computer Algebra: Fast
Marc Moreno Maza
2007-01-10
![]() R[x]
R[x]
![]() R
R
![]() (n2)
(n2)
![]() (n log(n)log(log(n)))
(n log(n)log(log(n)))