We consider the following algorithm, which computes the gcd of two integer numbers.
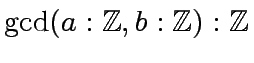 ==
==
1 if 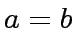 then return
then return 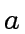
2 if
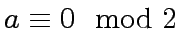 and
and
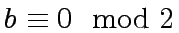 then return
then return
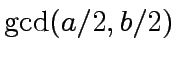
3 if
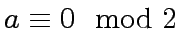 and
and
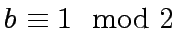 then return
then return
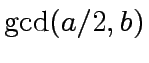
3 if
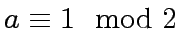 and
and
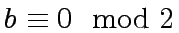 then return
then return
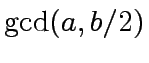
4 if 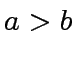 then return
then return
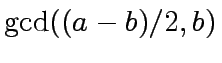 else return
else return
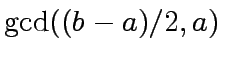
- Let
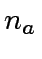 and
and 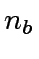 the number of bits (in binary-expansion) of
the number of bits (in binary-expansion) of 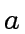 and
and 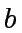 respectively.
Give an upper bound for the number of reursive calls needed to compute
respectively.
Give an upper bound for the number of reursive calls needed to compute
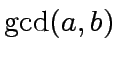 ?
?
- Give an upper bound for the number of machine word operations needed for
computing
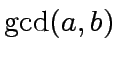 .
.
Answer 2

Answer 3

Marc Moreno Maza
2008-01-31
==
then return
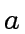
and
then return
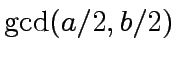
and
then return
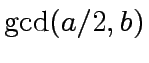
and
then return
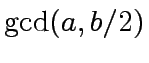
then return
else return
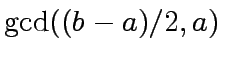
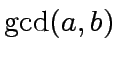 ?
?
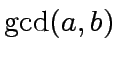 .
.