Let 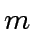 and
and 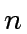 be two relatively prime elements of an Euclidean domain
be two relatively prime elements of an Euclidean domain 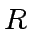 .
(You may think
.
(You may think
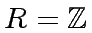 or
or
![$ R = {\mbox{${\mathbb{Q}}$}}[x]$](img13.png) .)
Let
.)
Let
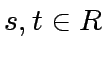 be such that
be such that
 .
For every
.
For every
 there exists
there exists  such that
such that
 |
(1) |
where a convenient 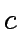 is given by
is given by
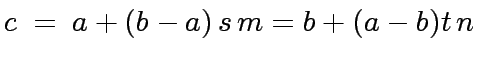 |
(2) |
Let 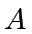 and
and 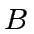 be two square matrices of order
be two square matrices of order 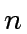 and with coefficients in
and with coefficients in
 where
where 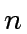 is a power of
is a power of 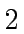 . We recall the Strassen's trick for computing
. We recall the Strassen's trick for computing  .
.
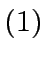
- If
 the matrices
the matrices  et
et  are of the form
are of the form 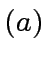 et
et 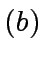 where
where
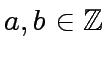 , such that
, such that 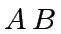 equals
equals 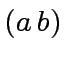 .
.
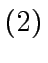
- If
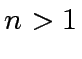 the matrices
the matrices 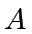 and
and 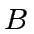 can be decomposed as
can be decomposed as
where 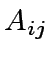 and
and 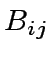 are square matrices
of order
are square matrices
of order 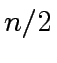 .
Then, one computes the following 8 sums.
.
Then, one computes the following 8 sums.

- Next, one computes the following 7 matrix products by recursive calls
to the algorithm.
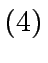
- Finally, one computes the following 7 sums:
and one returns:
Next, we recall the Extended Euclidean Algorithm.
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $a,b \in ...
...$\ \\
\> {\bf return}($r_{i-2}, s_{i-2}, t_{i-2}$)
\end{tabbing}\end{minipage}}](img44.png)
Marc Moreno Maza
2008-01-31
![$ R = {\mbox{${\mathbb{Q}}$}}[x]$](img13.png) .)
Let
.)
Let
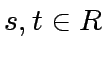 be such that
be such that
 .
For every
.
For every
 there exists
there exists  such that
such that

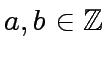 , such that
, such that 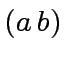 .
.
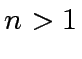 the matrices
the matrices 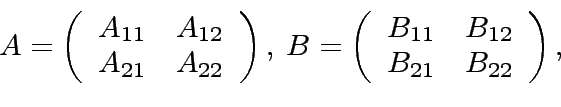
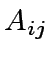 and
and 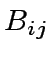 are square matrices
of order
are square matrices
of order 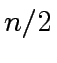 .
Then, one computes the following 8 sums.
.
Then, one computes the following 8 sums.
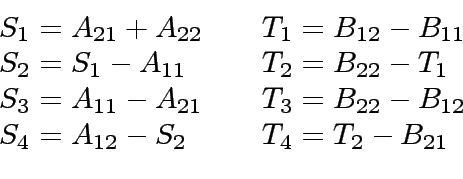
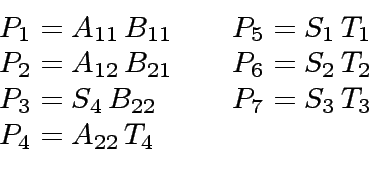
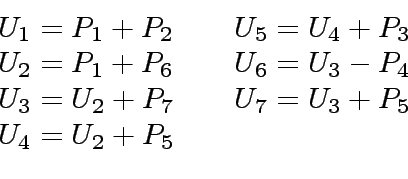
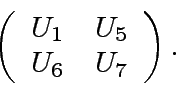
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $a,b \in ...
...$\ \\
\> {\bf return}($r_{i-2}, s_{i-2}, t_{i-2}$)
\end{tabbing}\end{minipage}}](img44.png)