Let
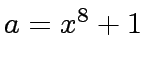 ,
,
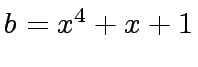 ,
,
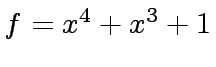 be in
be in
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img20.png) .
.
- Compute the inverse of
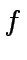 modulo
modulo 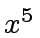 .
.
- Deduce the quotient and the remainder in the Euclidean
division of
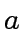 w.r.t.
w.r.t. 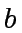 .
.
Note that the example has been chosen such that computations
can easily be carried out by hand.
Answer 1

Answer 2

Marc Moreno Maza
2008-01-31
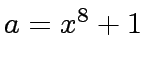 ,
,
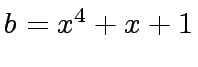 ,
,
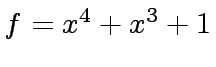 be in
be in
![$ {\mbox{${\mathbb{Q}}$}}[x]$](img20.png) .
.