

Next: Exercise 4
Up: The Assignment
Previous: Exercise 2
We consider the grammar G with
- the six terminals ( , ) ,
 ,
,
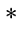 ,
,  and
and  (the opening parenthesis, the closing parenthesis, the pipe, the star, the lower-case letter a, the lower-case letter b)
(the opening parenthesis, the closing parenthesis, the pipe, the star, the lower-case letter a, the lower-case letter b)
- the non-terminal and start symbol R
- the six productions below
| R |
 |
R
 R R |
| R |
 |
R R |
| R |
 |
R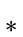 |
| R |
 |
(R) |
| R |
 |
 |
| R |
 |
 |
Let 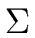 be the alphabet consisting
of the six terminals of G. Hence
be the alphabet consisting
of the six terminals of G. Hence
Let L be the language over 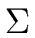 generated by G.
generated by G.
- Is the language L regular?
- Show that the language L is context-free.
- Construct a parse tree for the expression
 (
(

 )
)
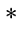 .
.
- Show that G is ambiguous.


Next: Exercise 4
Up: The Assignment
Previous: Exercise 2
Marc Moreno Maza
2004-12-01