


Next: Data-flow analysis: copy propagation.
Up: Compiler Theory: Code Optimization
Previous: Data-flow analysis: identifying loops
Recall that we consider a TAC program  .
We assume that it is generated from a high level
language where statements are
.
We assume that it is generated from a high level
language where statements are
- assignments,
- alternatives,
- while loops.
So our high level program may be generated by a grammar of the form
| S |
 |
id := E |
| S |
 |
S ; S |
| S |
 |
if E then S else S |
| S |
 |
while E do S |
| E |
 |
E + E |
| E |
 |
E - E |
| E |
 |
E = E |
| E |
 |
E < E |
| E |
 |
id |
| E |
 |
num |
| E |
 |
bool |
Hence we can assume that the control flow graph G of  is reducible.
Moreover we assume that
is reducible.
Moreover we assume that
- the assignments of our TAC are of one of the forms
- x := y,
- x := unop y where unop is a unary arithmetic operation,
- x := y binop z where binop is a binary arithmetic operation.
- and all other statements are conditional or unconditional jumps.
(Hence we do not consider pointers nor function calls.)
Finally we assume that the alternatives and while loops
are translated using the translation schemes of the previous
chapter. This implies that whatever is E the control
will flow to the same point after executing each of the statements.
- if E then S1 else S2
- while E do S
POINTS. Within a basic block B, a point denotes
- either the beginning of B (before its first statement)
- or the end of a statement.
Hence each basic block consisting of  statements possesses
statements possesses
 + 1 points. We will use the following notations.
+ 1 points. We will use the following notations.
- The first point of B is denoted by first(B).
- The last point of B is denoted by last(B).
PATH. A sequence of points
p1,..., pn is a path if for
every
i = 1,..., n - 1
- either pi and pi+1 are in the same basic bloc
and pi immediately precedes pi+1.
- or pi is the last point of a block B and pi+1
is the first point a block B' such that there is an edge
from B to B' in G.
VARIABLE DEFINITION. A definition of a variable x is a statement that assigns
(or may assign) x.
Observations.
- Because of our assumptions regarding TAC a statement assign or does
not assign a variable.
- In a more general theory, with procedure calls or pointers,
a statement may assign a variable. In this case we would
consider the notions of unambiguous definitions and ambiguous definitions.
A VARIABLE DEFINITION D REACHES A POINT P if there is a path from the point immediately following d to p
such that d is not modified (killed) along this path.
From now
- we number each TAC statement and
- we will refer to a variable definition by the number of the statement
where this definition is made.
REGION. A subgraph R of the control flow graph G is a region of G
if there exists a unique node h of R which dominates
all other nodes of R.
Observations.
- This unique point h is called the header of the region.
- A loop is a special case of a region that is strongly
connected.
Theorem 1
The subgraph of the CFG corresponding to the
translation of a statement
S of our high level
language is a region denoted by
region(
S).
Moreover, by introducing empty blocks, one
may assume that
for any statement S of our high level language
control can flow to only
one outside block when it leaves region(S).
A STATEMENT REGION is a subgraph of the CFG of the form region(S).
Because of the previous definition and theorem,
it makes sense to talk about the first point
and the last point of a region,
denoted respectively by
entry(S) and exit(S).
DATA-FLOW SETS FOR STATEMENT REGIONS. For each statement S of our high level program,
we associate four sets to region(S).
Each of them
- is a subset of the variable definitions of the
TAC program
 and
and
- can be viewed as an attribute of the statement S.
These sets are defined as follows.
- in(S):
- A definition d (from anywhere in
 ) belongs to in(S)
if d is active at
entry(S).
) belongs to in(S)
if d is active at
entry(S).
- out(S):
- A definition d (from anywhere in
 ) belongs to out(S)
if d is active at exit(S).
) belongs to out(S)
if d is active at exit(S).
- gen(S):
- A definition d belongs to gen(S) if d is made
in S and there exists a path from to d to exit(S)
which uses points all inside S.
- kill (S):
- A definition d (from anywhere in
 )
belongs to kill (S) if for every path from
entry(S) to exit(S)
it is killed by definition d' with d
)
belongs to kill (S) if for every path from
entry(S) to exit(S)
it is killed by definition d' with d  d'.
d'.
Observe that these definitions extend naturally to basic blocks
since a basic block can be viewed as a sequence of statements of the
high level language.
DATA-FLOW EQUATIONS. We give below equations relating the data-flow sets.
- It is important to realize that these equations are an approximation
of what will really happen when the programs runs.
Indeed some killing statements may in fact
not kill like in
x := 0
y := y + x
- A central principle of code improving transformations
is that we should make conservative decisions
- if in doubt we should add a statement to a generated set
- if in doubt, we should not add any definition to a killed set.
DATA-FLOW EQUATIONS FOR AN ASSIGNMENT.
| gen(S) |
= |
{d} |
| kill (S) |
= |
Da  {d} {d} |
| out(S) |
= |
gen(S)  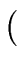 in(S) in(S)  kill (S) kill (S)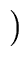 |
|
(1) |
where Da denotes the set of all definitions of a in the TAC program  .
Figure 6 illustrates the fact that gen(S), kill (S), out(S)
can be computed from in(S).
.
Figure 6 illustrates the fact that gen(S), kill (S), out(S)
can be computed from in(S).
Figure 6:
Data-flow equations for an assignment.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{assignmentDataFlowEq.eps}
\end{figure}](img18.png) |
DATA-FLOW EQUATIONS FOR A SEQUENCE OF STATEMENTS.
| gen(S) |
= |
gen(S2)  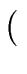 gen(S1) gen(S1)  kill (S2) kill (S2)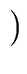 |
| kill (S) |
= |
kill (S2)   kill (S1) kill (S1)  gen(S2) gen(S2)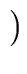 |
| in(S1) |
= |
in(S) |
| in(S2) |
= |
out(S1) |
| out(S) |
= |
out(S2) |
|
(2) |
Figure 7 illustrates the fact that gen(S), kill (S), out(S)
are synthesized attributes whereas in(S) is an inherited attribute.
Figure 7:
Data-flow equations for a sequence of statements.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{statementsDataFlowEq.eps}
\end{figure}](img23.png) |
DATA-FLOW EQUATIONS FOR AN ALTERNATIVE.
| gen(S) |
= |
gen(S1)  gen(S2) gen(S2) |
| kill (S) |
= |
kill (S1)  kill (S2) kill (S2) |
| in(S1) |
= |
in(S) |
| in(S2) |
= |
in(S) |
| out(S) |
= |
out(S2)  out(S1) out(S1) |
|
(3) |
Figure 8:
Data-flow equations for an alternative.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{alternativeDataFlowEq.eps}
\end{figure}](img25.png) |
DATA-FLOW EQUATIONS FOR A WHILE LOOP.
| gen(S) |
= |
gen(S1) |
| kill (S) |
= |
kill (S1) |
| in(S1) |
= |
in(S)  gen(S1) gen(S1) |
| out(S) |
= |
out(S1) |
|
(4) |
Observe that syntax-directed definition associated
with the above rules is not L-attributed.
Indeed, the inherited attribute in(S1) depends on the
synthesized attribute gen(S1).
Figure 9:
Data-flow equations for a while loop.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.45]{whileDataFlowEq.eps}
\end{figure}](img26.png) |
COMPUTING THE DATA-FLOW SETS.
- The synthesized attributes gen(S) and kill (S) can be computed
during a bottom-up parsing
- However the inherited attributes in(S) cannot be computed
by a depth-first traversal of the parse tree because of the rule
in(S1) = in(S)  gen(S1) gen(S1) |
(5) |
as mentioned above.
- To compute the inherited attributes in(S) we use a completion
algorithm as for the FOLLOW sets or the dominator sets.
- This is done by Algorithm 4 which assumes
that the sets kill (B) and gen(B) are known for every basic bloc B.
Algorithm 4
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $kill(B)$...
...cup} \ \left( in(B) \setminus kill(B) \right)$\ \\
\end{tabbing}\end{minipage}}](img27.png)
Observations.
- Since each
| out(B) | is bounded (by the number of lines of the TAC program)
and since there is a finite number of basic blocks,
the algorithm has to stop.
- When it stops, the sets in(B) cannot further increase since
the sets out(B) are themselves saturated.
- One can show (not really difficult) that this algorithm has a quadratic time
complexity in the number of lines of the
 program.
program.
- This algorithm can be implemented efficiently by coding
each data-flow set by an inetger (regarded as a bit vector)
and using bit vector operation from the machine processor.
- Algorithm 5 detects loop invariant computations.
Algorithm 5
![\fbox{
\begin{minipage}{13 cm}
\begin{description}
\item[{\bf Input:}] A loop $L...
...\\
\> \> \> \> which is marked {\sc INVARIANT} \\
\end{tabbing}\end{minipage}}](img28.png)
Note that a loop invariant is not necessarily a TAC which can be moved
into a pre-header. Indeed, in a given loop we may have two statemens with constant operands
that define the same variable. For instance, x := 2 and x:= 5.



Next: Data-flow analysis: copy propagation.
Up: Compiler Theory: Code Optimization
Previous: Data-flow analysis: identifying loops
Marc Moreno Maza
2004-12-02
 gen(S1)
gen(S1)