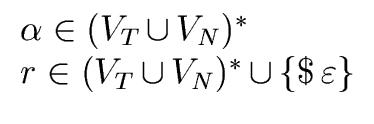Next: LL(1) Grammars
Up: Parsing
Previous: Predictive parsing
THE IDEA.
Predictive parsing can be performed using a pushdown stack,
avoiding recursive calls.
- Initially the stack holds just the start symbol of the grammar.
- At each step a symbol X is popped from the stack:
- if X is a terminal symbol then it is matched with
lookahead and lookahead is advanced,
- if X is a nonterminal, then using lookahead and a parsing table
(implementing the FIRST sets)
a production is chosen and its right hand side is pushed onto the stack.
- This process goes on until the stack and the input string become empty.
It is useful to have an end_of_stack and an end_of_input
symbols. We denote them both by $.
Figure 8
shows the structure of non-recursive predictive parsers.
For each nonterminal A and each token a
the entry M[A, a] of the parsing table contains either
an A-production generating sentences starting with a
or an error-entry.
Figure 8:
The structure of non-recursive predictive parsers.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{nonRecursivePredictiveParsing.eps}
\end{figure}](img125.png) |
Example 17
Consider the grammar G given by:
|
S |
 |
aAa | BAa |  |
|
A |
 |
cA | bA |  |
|
B |
 |
b |
|
a |
b |
c |
$ |
|
S |
S  aAa aAa |
S  BAa BAa |
|
S   |
|
A |
A  
|
A  bA bA |
A  cA cA
|
|
|
B |
|
B  b b |
|
|
|
Stack |
Remaining input |
action |
|
$S |
bcba$ |
choose
S  BAa BAa |
|
$aAB |
bcba$ |
choose
B  b b |
|
$aAb |
bcba$ |
match b |
|
$aA |
cba$ |
choose
A  cA cA |
|
$aAc |
cba$ |
match c |
|
$aA |
ba$ |
choose
A  bA bA |
|
$aAb |
ba$ |
match b |
|
$aA |
a$ |
choose
A   |
|
$a |
a$ |
match a |
THE ALGORITHM.
Algorithm 5

COMPUTING THE FIRST SETS.
Recall that for any string  of symbols the set FIRST(
of symbols the set FIRST( )
satisfies the following conditions for every terminal a and every string of symbols
)
satisfies the following conditions for every terminal a and every string of symbols 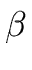
- FIRST(
 )
)
 VT
VT  {
{ }
}
-

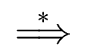 a
a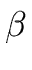 iff a
iff a  FIRST(
FIRST( )
)
-


 iff
iff

 FIRST(
FIRST( ).
).
For a symbol
X  VT
VT  VN the set FIRST(X) can be computed as follows
VN the set FIRST(X) can be computed as follows
Algorithm 6
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] $X \in V_...
...) := {\sc FIRST}($X$) ${\cup} \ \{ {\varepsilon} \}$\end{tabbing}\end{minipage}}](img127.png)
Comments about the computation of FIRST(X) with Algorithm 6.
- The case where X is a terminal symbol is trivial.
- Assume from now on that X is a nonterminal.
The case where
X

 follows
immediately from the specifications of FIRST(X).
follows
immediately from the specifications of FIRST(X).
- Assume that there is a production of the form
X
 X1X2 ... Xk
where
X1, X2,...Xk are grammar symbols.
If
X1X2 ... Xk
where
X1, X2,...Xk are grammar symbols.
If

 FIRST(X1) then
the first letter of a word generated from
X1X2 ... Xk
is the first letter of a word generated from X1 and thus
FIRST(X) = FIRST(X1).
If
FIRST(X1) then
the first letter of a word generated from
X1X2 ... Xk
is the first letter of a word generated from X1 and thus
FIRST(X) = FIRST(X1).
If

 FIRST(X1) but
FIRST(X1) but

 FIRST(X2) then
the first letter of a word generated from
X1X2 ... Xk
is either the first letter of a word generated from X1
or the first letter of a word generated from X2.
Etc ...
This explains the nested for loop.
FIRST(X2) then
the first letter of a word generated from
X1X2 ... Xk
is either the first letter of a word generated from X1
or the first letter of a word generated from X2.
Etc ...
This explains the nested for loop.
- The last if statement tells that if
 belongs to all
FIRST(Xi) then
belongs to all
FIRST(Xi) then
 must be in FIRST(X).
This statement is necessary since the nested for loop cannot
add
must be in FIRST(X).
This statement is necessary since the nested for loop cannot
add
 to FIRST(X) even if
to FIRST(X) even if
 belongs to all
FIRST(Xi).
belongs to all
FIRST(Xi).
Algorithm 7
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $X = X_1 ...
...) := {\sc FIRST}($X$) ${\cup} \ \{ {\varepsilon} \}$\end{tabbing}\end{minipage}}](img129.png)
The principle of Algorithm 7
is similar to that of Algorithm 6.
- If

 FIRST(X1) then
the first letter of a word generated from
X1X2 ... Xk
must be the first letter of a word generated from X1.
FIRST(X1) then
the first letter of a word generated from
X1X2 ... Xk
must be the first letter of a word generated from X1.
- If

 FIRST(X1) but
FIRST(X1) but

 FIRST(X2) then
the first letter of a word generated from
X1X2 ... Xk
is either the first letter of a word generated from X1
or the first letter of a word generated from X2.
FIRST(X2) then
the first letter of a word generated from
X1X2 ... Xk
is either the first letter of a word generated from X1
or the first letter of a word generated from X2.
- Etc ...
-
 belongs to FIRST(
X1X2 ... Xk)
iff it belongs to each FIRST(Xi).
belongs to FIRST(
X1X2 ... Xk)
iff it belongs to each FIRST(Xi).
THE FOLLOW SETS. In order to give an algorithm
for building the parsing table we define for every A  VN
VN
FOLLOW(A) =  a a  VT VT  {$} | S$ {$} | S$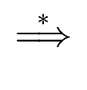  Aar | Aar | 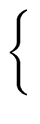 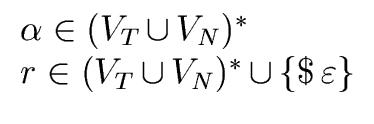 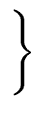 |
(42) |
In other words FOLLOW(A) is the set of the terminals that can appear
immediately to the right of the nonterminal A in some sentential form.
Moreover $ belongs to FOLLOW(A) if A is the rightmost
symbol in some sentential form.
COMPUTING THE FOLLOW SETS.
Algorithm 8
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] $G = (V_T...
...{\bf then} \\
\> \> \> \> \> $done$\ := {\bf true}
\end{tabbing}\end{minipage}}](img134.png)
The FOLLOW sets of all nonterminal symbols are computed together
by the following process:
- Initially all these sets are empty, except FOLLOW(S).
- There exist three rules that can increase FOLLOW(B)
for a given nonterminal B.
These rules are:
- if
(A

 B
B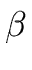 ) then FOLLOW(B) :=
FIRST(
) then FOLLOW(B) :=
FIRST(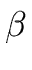 )
)  {
{ }
}  FOLLOW(B)
FOLLOW(B)
- if
(A

 B) then FOLLOW(B) := FOLLOW(B)
B) then FOLLOW(B) := FOLLOW(B)  FOLLOW(A)
FOLLOW(A)
- if
(A

 B
B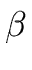 ) and
) and
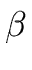

 then FOLLOW(B) := FOLLOW(B)
then FOLLOW(B) := FOLLOW(B)  FOLLOW(A)
FOLLOW(A)
- Let us call a pass the fact of trying to apply each rule to each nonterminal.
- Then the algorithm scheme can be stated as follows:
repeat perform a pass until this pass does not change
any of the FOLLOW sets.
- To implement this process in Algorithm 8 we use two boolean
auxiliary variables:
- done which becomes true when a pass could not increase any of the FOLLOW sets.
- building which becomes true during a pass if at least one FOLLOW set could
be increased.
- In the pseudo-code of Algorithm 8 the value
| FOLLOW(B) | denotes the number
of elements of the set FOLLOW(B).
- One could wonder whether Algorithm 8 could run forever.
But it is easy to see that the process has to stop.
Indeed, each FOLLOW set contains at most t + 1 symbols
where t is the number of terminals.
So the number of passes is at most n(t + 1) where n is the
number of nonterminals (since each successful pass increases at least
by one the number of elements of at least one FOLLOW set).
COMPUTING THE PARSING TABLE.
Algorithm 9
![\fbox{
\begin{minipage}{10 cm}
\begin{description}
\item[{\bf Input:}] $G = (V_T...
...} \\
\> \> \> \> \> \> \> $M[A,a]$\ := {\em error}
\end{tabbing}\end{minipage}}](img136.png)
Algorithm 9 consists of three main steps.
- The first for loop which initializes each entry of
the parsing table M to the empty set.
- The second for loop which fills the parsing table M
by using the following rules.
- If
A

 with
with


 is a production and if a is a terminal such that
a
is a production and if a is a terminal such that
a  FIRST(
FIRST( )
then the production
A
)
then the production
A 
 is added to M[A, a].
is added to M[A, a].
- If

 FIRST(
FIRST( )
(which means
)
(which means


 )
then the production
A
)
then the production
A 
 is added to M[A, b] for every
b
is added to M[A, b] for every
b  FOLLOW(A).
In particular if
FOLLOW(A).
In particular if

 FIRST(
FIRST( )
and
$
)
and
$  FOLLOW(A)
then the production
A
FOLLOW(A)
then the production
A 
 is added to M[A,$].
is added to M[A,$].
- The third for loop which sets to error every empty entry
of the parsing table M.
Example 19
Consider the following grammar (with terminals
+ ,*,(,), and nonterminals
T, E, E', F)
and nonterminals
T, E, E', F)
|
E |
 |
TE' |
|
E' |
 |
+ TE' |  |
|
T |
 |
FT' |
|
T' |
 |
*FT' |  |
|
F |
 |
(E) |  |
|
FIRST(F) |
= |
{(, } } |
|
FIRST(T) |
= |
{(, } } |
|
FIRST(T') |
= |
{*, } } |
|
FIRST(E) |
= |
{(, } } |
|
FIRST(E') |
= |
{ + , } } |
|
FIRST(TE') |
= |
{(, } } |
|
FIRST(FT') |
= |
{(, } } |
|
FIRST((E)) |
= |
{(} |
|
FIRST(+ TE') |
= |
{ + } |
|
FIRST(*FT') |
= |
{*} |
|
FOLLOW(E) |
= |
{),$} |
|
FOLLOW(E') |
= |
{),$} |
|
FOLLOW(T) |
= |
{ + ,),$} |
|
FOLLOW(T') |
= |
{ + ,),$} |
|
FOLLOW(F) |
= |
{ + ,*,),$} |
|
 |
+ |
* |
( |
) |
$ |
|
E |
E  TE' TE' |
|
|
E  TE' TE' |
|
|
|
E' |
|
E'  + TE' + TE' |
|
|
E'   |
E'   |
|
T |
T  FT' FT' |
|
|
T  FT' FT' |
|
|
|
T' |
|
T'   |
T'  *FT' *FT' |
|
T'   |
T'   |
|
F |
F   |
|
|
F  (E) (E) |
|
|
Example 20
Consider the following grammar (with terminals
a, b, e, i, t and nonterminals S, S', E)
|
S |
 |
i E t S S' | a |
|
S' |
 |
e S |  |
|
E |
 |
b |
|
FIRST(
i E t S S') |
= |
{i} |
|
FIRST(a) |
= |
{a} |
|
FIRST(e S) |
= |
{e} |
FIRST(
 ) ) |
= |
{ } } |
|
FIRST(b) |
= |
{b} |
| if |
A   B B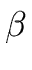 |
then |
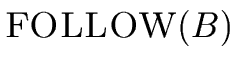 : = : =   { { } }  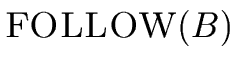 |
| if |
A   B B |
then |
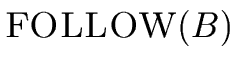 : = : = 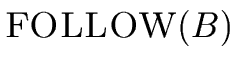  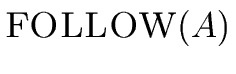 |
| if |
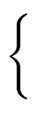 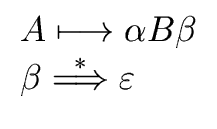 |
then |
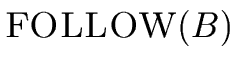 : = : = 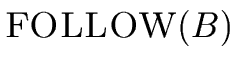  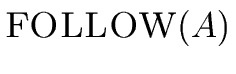 |
|
(43) |
|
Initialization |
S  iEtSS' iEtSS' |
S  iEtSS' iEtSS' |
|
FOLLOW(S) |
{$} |
{e,$} |
{e,$} |
|
FOLLOW(S') |
 |
 |
{e,$} |
|
FOLLOW(E) |
 |
{t} |
{t} |
|
a |
b |
e |
i |
$ |
t |
|
S |
S  a a |
|
|
S  iEtSS' iEtSS' |
|
|
|
S' |
|
|
S'   |
|
S'   |
|
|
|
|
S'  eS eS |
|
|
|
|
E |
|
E  b b |
|
|
|
|
-
S'
 eS (since
e
eS (since
e  FIRST(e S))
FIRST(e S))
-
S'

 (since
(since

 FIRST(
FIRST(
 )
and since
e
)
and since
e  FOLLOW(S'))
FOLLOW(S'))
We know that this grammar is ambiguous and this ambiguity is shown by this choice
of productions when an e (else) is seen.
ERROR RECOVERY IN PREDICTIVE PARSING. A predictive parser attempts to match the nonterminals and the terminals
in the stack with the remaining input.
Therefore two types of conflicts can occur.
- T-conflict.
- A terminal appearing on top of the stack does not match the following
input token.
- N-conflict.
- For a nonterminal B on top of the stack and the lookahead token b
the entry M[B, b] of the parsing table is empty.
Panic-mode recovery is based on the idea of skipping symbols
on the input string until a token in a selected set of synchronizing tokens appears.
These synchronizing sets should be chosen such that the parser recovers quickly
from errors that are likely to occur in practice.
Here are some strategies for the above conflict cases.
- T-conflict.
- Skip (= ignore and advance) the token in the input string.
Hence the synchronizing set conists here of all other tokens.
- N-conflict.
- Possible solutions.
- Skip (= ignore and advance) the token b in the input string.
- If M[B, b] is a blank entry labeled synch then skip (= pop and ignore)
the nonterminal B. (Strictly speaking and according to the above definition,
this is not a panic-mode recovery, but quite close in the spirit.)
- Skip tokens from the input string until an element of FIRST(B)
is reached, then continue parsing normally.
So the synchronizing set here is FIRST(B).
- Skip tokens from the input string until an element of FOLLOW(B)
is reached, then skip B and continue parsing normally.
(Again this is a variation of panic-mode recovery.)
- Delimiters such as ; in C can be added to the two previous synchronizing sets.



Next: LL(1) Grammars
Up: Parsing
Previous: Predictive parsing
Marc Moreno Maza
2004-12-02
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{nonRecursivePredictiveParsing.eps}
\end{figure}](img125.png)
![]() of symbols the set FIRST(
of symbols the set FIRST(![]() )
satisfies the following conditions for every terminal a and every string of symbols
)
satisfies the following conditions for every terminal a and every string of symbols ![]()
![]() VN
VN