


Next: Chomsky classification
Up: Grammars and Parsing
Previous: An introduction to the notion
A GRAMMAR is quadruple
(VT, VN, S, P) such that
- VT is a finite set of symbols called terminals,
- VN is a finite set of symbols called non-terminals,
- S is a distinguished non-terminal called start-symbol,
- P is a finite set of couples
(
 ,
,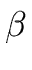 )
called productions where
)
called productions where
 and
and 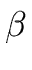 belong
to
(VT
belong
to
(VT  VN) * and
VN) * and
 does not belong
(VT) * .
does not belong
(VT) * .
In other words a production is made of two words over
the alphabet
VT  VN such that
the first word contains at least one non-terminal symbol.
The set
VT
VN such that
the first word contains at least one non-terminal symbol.
The set
VT  VN is called the set
of grammar symbols.
VN is called the set
of grammar symbols.
Notation 1
Here are some usual notational conventions about grammars.
- It is convenient to denote a production


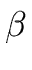 instead of
(
instead of
( ,
,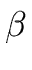 ).
).
- By default, the following symbols are terminals:
lower-case letters, arithmetic operators, punctuation symbols,
digits and boldface strings (if, id, ...).
- By default, the following symbols are non-terminals:
upper-case letters early in the alphabet such as
A, B, C,...,
the letter S (for the start-symbol), lower-case italic names
such as stmt, expr.
- By default, the following symbols are grammar symbols:
upper-case letters late in the alphabet such as X, Y, Z
- By default, strings of terminals are denoted by
lower-case letters late in the alphabet such as u, v, w.
- By default, strings of grammar symbols are denoted by
lower-case Greek letters early in the alphabet
such as
 ,
,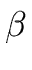 ,
, .
.
- By default, the start symbol is the left side of the first production.
- If
A

 ,
A
,
A 
 , ...
A
, ...
A 
 are all the productions with A
as their left side (these productions are called A-productions)
then we can write
A
are all the productions with A
as their left side (these productions are called A-productions)
then we can write
A 
 |
|  | ... |
| ... |  .
The sequence
.
The sequence
 |
|  | ... |
| ... |  is called the alternatives of A.
is called the alternatives of A.
Example 2
Using the conventions of Notation
1
the grammar of Example
1
can be stated as follows
| E |
 |
E A E | (E) | -E | id |
| A |
 |
+ | - | * | / |  |
Remark 2
Grammars offer significant advantages to both language
designers and compiler writers. Among them
- A grammar gives a precise and easy to understand syntactic specification
of a programming language.
- From certain classes of grammars we can automatically
construct an efficient parser that determines if a source
program is syntactically well formed.
- Developing a language given by a grammar
(adding or removing constructs) is easy.
DERIVATIONS. Let
G = (VT, VN, S, P) be a grammar
and let  and
and 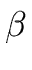 be two strings of grammar symbols for G.
We say that
be two strings of grammar symbols for G.
We say that 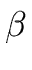 derives from
derives from  in one step
and we write
in one step
and we write


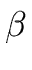 if there exist strings of grammar symbols
if there exist strings of grammar symbols
 ,
,

 ,
,  , such that
, such that
-
 =
= 

 ,
,
-
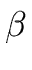 =
= 

 ,
,
-


 is a production of G.
is a production of G.
The transitive and reflexive closure of the
map
( ,
,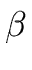 )
) 


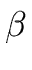 over the sets of grammar symbols is denoted by
(
over the sets of grammar symbols is denoted by
( ,
,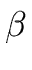 )
) 

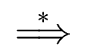
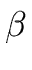 .
Thus for two grammar symbols
.
Thus for two grammar symbols  and
and 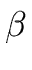 we have
we have
Intuitively,


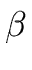 means that
means that 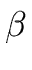 derives from
derives from  in a finite number of steps.
A sequence of strings of grammar symbols
(
in a finite number of steps.
A sequence of strings of grammar symbols
( ,
, ,...,
,..., )
is a DERIVATION if we have
)
is a DERIVATION if we have
THE LANGUAGE GENERATED BY A GRAMMAR. Let
G = (VT, VN, S, P) be a grammar.
The language over VT generated by G and denoted by L(G)
is the set of the words w of
VT * such that
S w.
The words of L(G) are called the sentences of G.
More generally any string of grammar symbols
w.
The words of L(G) are called the sentences of G.
More generally any string of grammar symbols  such that
S
such that
S
 is called
a sentential form of G.
is called
a sentential form of G.
A language L over the alphabet
 = VT is said
formal if there exists a grammar G such that
L is generated by G.
Observe that
= VT is said
formal if there exists a grammar G such that
L is generated by G.
Observe that
- Some languages are not formal like natural languages.
- Two different sequences of derivations-in-one-step can
lead to the same sentential form.
- Moreover, two different grammars can generate the same language.
These last two observations are illustrated by
Example 3.
Example 3
Let us consider again arithmetic expressions.
For simplicity we consider only two operations + and *.
Our language L can be generated by the grammar G1:
| expr |
 |
expr + expr | expr * expr | (expr) | id |
| expr |
 |
expr + term | term |
| term |
 |
term * factor | factor |
| factor |
 |
(expr) | id |
Consider now the arithmetic expression
 +
+  *
* .
Two different sequences of derivations-in-one-step of G1 can lead to it:
.
Two different sequences of derivations-in-one-step of G1 can lead to it:
This is sketched
by the trees of Figure 2, called parse trees.
Figure 2:
Two parse trees for the same sentence.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{twoParseTrees.eps}
\end{figure}](img42.png) |
With G2 several derivations-in-one-step can lead to
 +
+  *
* .
However they all correspond to the same tree
shown on Figure 3.
.
However they all correspond to the same tree
shown on Figure 3.
Figure 3:
The parse tree of
 +
+  *
* with G2.
with G2.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.5]{oneParseTree.eps}
\end{figure}](img44.png) |
This notion of a parse tree is formalized later.
NON-TERMINALS can be seen as syntactic variables
that denote the sets of strings that can be derived from them.
They also impose a hierarchical structure on the language
that is useful for both syntax analysis and translation.
Moreover Example 3
shows that an accurate use of non-terminals can reduce
ambiguity.



Next: Chomsky classification
Up: Grammars and Parsing
Previous: An introduction to the notion
Marc Moreno Maza
2004-12-02
 and
and 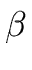 belong
to
(VT
belong
to
(VT  VN) * and
VN) * and
 does not belong
(VT) * .
does not belong
(VT) * .
![]() and
and ![]() be two strings of grammar symbols for G.
We say that
be two strings of grammar symbols for G.
We say that ![]() derives from
derives from ![]() in one step
and we write
in one step
and we write
![]()
![]()
![]() if there exist strings of grammar symbols
if there exist strings of grammar symbols
![]() ,
,
![]()
![]() ,
, ![]() , such that
, such that
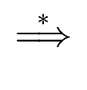



 ...
... 
![]() w.
The words of L(G) are called the sentences of G.
More generally any string of grammar symbols
w.
The words of L(G) are called the sentences of G.
More generally any string of grammar symbols ![]() such that
S
such that
S![]()
![]() is called
a sentential form of G.
is called
a sentential form of G.
![]() = VT is said
formal if there exists a grammar G such that
L is generated by G.
Observe that
= VT is said
formal if there exists a grammar G such that
L is generated by G.
Observe that