

Next: Specification of a Simple Type
Up: Compiler Theory: Type Checking
Previous: Compiler Theory: Type Checking
SEMANTIC CHECKING.
A compiler must perform many semantic checks on a source program.
- Many of these are straightforward and are usually done in conjunction with syntax-analysis.
- Checks done during compilation are called static checks
to distinguish from the dynamic checks done during the execution
of the target program.
- Static checks include:
- Type checks.
- The compiler checks that names and values are used in accordance with type rules of the language.
- Type conversions.
- Detection of implicit type conversions.
- Dereferencing checks.
- The compiler checks that dereferencing is applied
only to a pointer.
- Indexing checks.
- The compiler checks that indexing is applied only
to an array.
- Function call checks.
- The compiler checks that a
function (or procedure) is applied
to the correct number and type of arguments.
- Uniqueness checks.
- In many cases an identifier must be declared exactly once.
- Flow-of-control checks.
- The compiler checks that if a statement causes
the flow of control to leave a construct, then there is a place to transfer this flow.
For instance when using break in C.
In this chapter we will focus on type checking and type conversions.
Most of the other static checks are easy to implement.
TYPE INFORMATION
may be needed for the code generation.
For instance, for the translation of overloaded symbols
like +.
Indeed, overloading may be accompanied by coercion of types,
where a compiler supplies an operator to convert an operand
into the type expected by the context.
OVERLOADED SYMBOLS AND POLYMORPHIC FUNCTIONS.
An overloaded symbol is a symbol that represent different
operations in different contexts.
This is different from a polymorphic function
which is a function whose body can be executed
with arguments of several types.
TYPES HAVE STRUCTURE.
Generally types are either basic or structured.
- Basic types are the atomic types with no internal structure.
For instance, in C: char, int, double, float, etc.
- Structured types are the types of constructs like arrays, sets, (typed) pointers,
structs, classes, and functions.
TYPE EQUIVALENCE.
Because of overloaded symbols and structured types,
we will be concerned with the non trivial problem of type equivalence.
- That is, given two language constructs, decide whether they have the same type.
- We will use the notion of a type expression.
TYPE EXPRESSION.
The idea is to associate each language construct with an expression describing its type
and so called type expression.
Type expressions are defined inductively from basic types and constants
using type constructors.
Here are the type constructors that we shall consider in the remaining of this chapter.
They are close to type constructors of languages like C or PASCAL.
- Basic types.
- char, int, double, float
are type expressions.
- Type names.
- It is convenient to consider that names of types
are type expressions.
- Arrays.
- If T is a type expression and n is an int
then
array(n, T)
is a type expression denoting the type
of an array with elements in T
and indicies in the range
0 ... n - 1.
- Products.
- If T1 and T2 are type expressions then
T1 × T2
is a type expression denoting the type
of an element of the Cartesian product of
T1 and T2.
We assume that products of more than two types are defined
in a similar way and that this product-operation
is left-associative.
Hence
(T1 × T2) × T3
and
T1 × T2 × T3
are equivalent.
- Records.
- If name1 and name2 are two type names,
if T1 and T2 are type expressions then
record(name1: T1, name2: T2)
is a type expression denoting the type
of an element of the Cartesian product of
T1 and T2.
The only difference between a record and a product is
that the fields of a record have names.
- Pointers.
- If T is a type expression, then
pointer(T)
is a type expression denoting the type
pointer to an object of type T.
- Function types.
- If T1 and T2
are type expressions then
T1
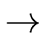 T2
T2
is a type expression denoting the type
of the functions associating an element from T1
with an element from T2.
GRAPHICAL REPRESENTATIONS FOR TYPE EXPRESSIONS.
Let
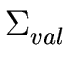 be the alphabet consisting of
be the alphabet consisting of
- the basic types,
- the possible values of an array index, say
 ,
,
- the possible names for a type.
Let
 be the alphabet consisting of
the keywords array, ×, record,
pointer and
be the alphabet consisting of
the keywords array, ×, record,
pointer and
 .
Then it is not hard to see that the set of type expressions
can be viewed as a language of expressions in the sense
of the section about syntax trees in the chapter
dedicated to syntax-directed definitions.
Indeed we could write
.
Then it is not hard to see that the set of type expressions
can be viewed as a language of expressions in the sense
of the section about syntax trees in the chapter
dedicated to syntax-directed definitions.
Indeed we could write
(array n T), (record name1 T1 name2 T2)
and (pointer T)
instead of
array(n, T), record(name1: T1, name2: T2) and
pointer(T).
That way we would satisfy the definition of a
language of (arithmetic) expressions.
It follows that we can use syntax trees and DAGs
to represent type expressions graphically.
TYPE SYSTEMS.
A type system is a set of rules assigning type
expressions to different parts of the program.
- Type systems can (usually) be implemented in a syntax-directed way.
- The implementation of a type system is called a type checker.
A LANGUAGE IS STRONGLY TYPED if the compiler can guarantee
that the accepted programs will execute without type errors.
Lisp languages are usually weakly typed:
CannaLisp listener 3.5 beta 2
-> (defun f (l) (car l))
f
-> (f '(+ 1 2))
+
-> (f (+ 1 2))
Bad arg to car 3


Next: Specification of a Simple Type
Up: Compiler Theory: Type Checking
Previous: Compiler Theory: Type Checking
Marc Moreno Maza
2004-12-02
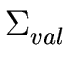 be the alphabet consisting of
be the alphabet consisting of
 be the alphabet consisting of
the keywords array, ×, record,
pointer and
be the alphabet consisting of
the keywords array, ×, record,
pointer and