|
P |
|
D |
|
D |
|
T |
T  |
|
E |
|
E |
|
E |
|
E |
|
E |
|
S |
|
S |
|
S |
|
S |
S 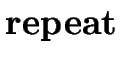 |
We consider the following grammar. As in the course, the nonterminals P, D, S, T, E stand for Program, Declaration, Statement, Type, Expression. The terminals id, boolean, integer, literal, num stand for identifier, boolean (as a type), integer (as a type), boolean literal (as a value), integer number (as a value).
|
P |
|
D |
|
D |
|
T |
T  |
|
E |
|
E |
|
E |
|
E |
|
E |
|
S |
|
S |
|
S |
|
S |
S 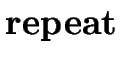 |
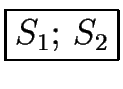 is that of S2.
is that of S2.
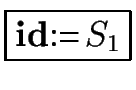 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
 is a valid
statement then its value is that of S1.
is a valid
statement then its value is that of S1.
 is valid as soon as
E.type =
is valid as soon as
E.type =  .
The attribute
.
The attribute
Question. Complete the following type checker for the above grammar.