

Next: Exercise 4.
Up: Quiz7
Previous: Exercise 2.
We extend the grammar of Exercise 2 in order
to handle unary functions with a single returned value.
Here's a program showing these new features.
f: integer -> integer;
f(n: integer): integer == {
if n = 0 then {1} else {n * f(n-1)};
}
To do so, we add productions for generating the type of a function,
the definition of a function, and a call to a function.
Here's the enhanced grammar.
P  D; S D; S |
D  D; D D; D |
D  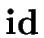 : T : T |
T  A A |
A  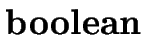 |
A   |
T  A1 A1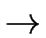 A2 A2 |
E  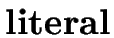 |
E  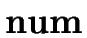 |
E  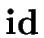 |
E  E1 E1 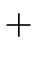 E2 E2 |
E  E1 E1 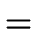 E2 E2 |
E  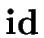  E1 E1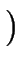 |
S  S1; S2 S1; S2 |
S  E E |
S  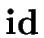 := S1 := S1 |
S  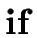 E E 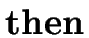  S1 S1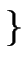 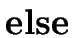  S2 S2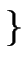 |
S  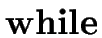 E E 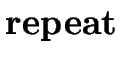  S1 S1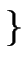 |
S  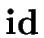  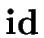 : A1 : A1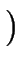 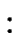 A2 = = A2 = =  S1 S1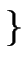 |
To keep things simple, observe that we impose the following constraints.
- (C1)
- The input type and the output type of a function can only
be primitive types, that is boolean or integer.
This appears in the above grammar.
- (C2)
- In our language, there is only one scope for
variables and functions. In other words, every variable
or function is global.
- (C3)
- In addition, each formal parameter of a function is
viewed as a variable.
These constraints imply that only one symbol table is needed,
as in the previous exercise.
To denote the type of a function you can use a record of the form
[in : T1, out : T2].
So, coming back to the above example
- parsing the first line would create an entry like
![\fbox{$f \ \mid \ [in: \, integer, out: \, integer]$}](img28.png) in the symbol table,
in the symbol table,
- parsing the function definition would create an entry like
 .
.
Finally, since in this language every statement has a value (see the previous exercise),
a function definition must have a value too. This value is simply the defined function.
So, coming back again to the above example, the type of the statement
corresponding to the function definition is just
[in : integer, out : integer].
Question. Complete the type checker for the following rules.
You can use any pseudo-code style that you like or even write sentences
like if there exists an entry e with type T then T.
Answer 3



Next: Exercise 4.
Up: Quiz7
Previous: Exercise 2.
Marc Moreno Maza
2004-12-02


![\fbox{$f \ \mid \ [in: \, integer, out: \, integer]$}](img28.png) in the symbol table,
in the symbol table,
 .
.