Projects aiming to apply the TRIADE technology in other problems

Project 5 (Lextriangular in MAPLE)   A first goal of this project is to implement in MAPLE the lextriangular of D. Lazard. Some of the functionalities of TRIADE can be used for this implementation. A second goal is to add an option which will guarantee that the output is a prime decomposition.

Project 6 (Computations with Algebraic Varieties based on TRIADE)   Based on the MAPLE or AXIOM version of TRIADE, the aim is to write a package for manipulating algebraic varieties. Each algebraic variety will be encoded by a square-free triangular decomposition. To save on the cost of factorization, these triangular decompositions will not be necessarily prime decompositions. The main operations provided by the package will be =, 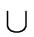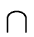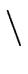$\cup$, $\cap$, $\setminus$ and the (explicit) Zariski closure of a quasi-component.

Project 7 (Optimized Pardi in MAPLE)   The PARDI algorithm is probably the best candidate for gaining a great speed up from the algorithms [HM02] and [MO04]. A first goal of this project is to implement the algebraic version of PARDI (called PALGIE) as an extension package of the MAPLE version of TRIADE. The second one is to measure the speed up obtained by calling the MAPLE implementations of the algorithms [HM02] and [MO04].