Project 10 (Task Management for T
RIADE in M
APLE)
The top level procedure of the TRIADE algorithm is a task manager,
which is meant to be implemented on a distributed environment.
Indeed, this procedure is a branch-and-cut algorithm.
This means that a running task T1 may be aborted before it is completed
because the completion of another running T2 shows that T1 is superfluous.
Therefore, performing
{T1, T2} in a distributed environment
will require less resources (time and space) than in a sequential one
starting with T1.
The key point for a sequential implementation is to develop strategies
that lead to perform T2 before T1.
The current implementations (AXIOM, ALDOR, MAPLE)
of the TRIADE algorithm are all sequential and
the goal of this project is to improve the existing strategies for avoiding
superfluous tasks.
The work will be on two fronts: algorithmic and experimental.
On the algorithmic front, a better understanding of the task generation
will be needed.
From there, one hopes to refine the existing strategies.
On the experimental front, one will have to measure the concrete
effect of the various strategies.
The experimentations will be conducted with the MAPLE version of TRIADE.
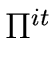 library.
library.