

Next: Exercise 2.
Up: Quiz1
Previous: Formulas.
Let n be an even positive integer.
Given two polynomials
r0, r1 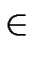
 [x] with respective degrees n and n/2,
we denote by D(n) the number of operations (additions, subtractions,
multiplications, inversions) in
[x] with respective degrees n and n/2,
we denote by D(n) the number of operations (additions, subtractions,
multiplications, inversions) in
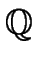 that are needed in order to compute
the quotient q2 and the remainder r2 of r0 by r1.
that are needed in order to compute
the quotient q2 and the remainder r2 of r0 by r1.
- What is the degree of q2? Give an estimation for D(n).
- Assume now that n is a power of 2, say n = 2k.
We run the Euclidean Algorithm starting from r0, r1.
Assume that the degree of each remainder ri+1 is half
the degree of the previous remainder ri.
Is the Euclidean Algorithm faster in this special case than in the usual one?
In other words, does the time complexity of the Euclidean Algorithm
becomes sub-quadratic, i.e.
O(n
 ) for some
) for some
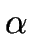 < 2?
< 2?
Answer 1



Next: Exercise 2.
Up: Quiz1
Previous: Formulas.
Marc Moreno Maza
2006-01-09