

Next: Exercise 3.
Up: Quiz1
Previous: Exercise 1.
Let k, n be two non-negative integers with n > 0.
Let
a, b 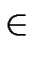
 [x] with respective degrees n + k and n.
Let D(n, k) the number of operations in
[x] with respective degrees n + k and n.
Let D(n, k) the number of operations in
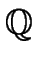 needed in order
to compute the quotient q and the remainder r of a by b
The polynomial b may not be monic.
needed in order
to compute the quotient q and the remainder r of a by b
The polynomial b may not be monic.
- If k = 0, how many operations in
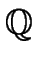 are needed to compute q only?
What is D(n, 0)?
are needed to compute q only?
What is D(n, 0)?
- If k = 1, show that one can compute q in at most 4 operations
in
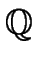 . What is D(n, 1)?
. What is D(n, 1)?
- How many operations in
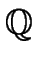 for computing q only if k = 2?
What is D(n, 2)?
for computing q only if k = 2?
What is D(n, 2)?
- Let Q(n, k) be the number operations in
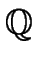 for computing q only.
Estimate Q(n, k) and D(n, k).
for computing q only.
Estimate Q(n, k) and D(n, k).
Answer 2

Answer 3



Next: Exercise 3.
Up: Quiz1
Previous: Exercise 1.
Marc Moreno Maza
2006-01-09