

Next: Modular Algorithms and interpolation
Up: The Euclidean Algorithm
Previous: The Extended Euclidean Algorithm
Let R be a (commutative) ring (with unity) and I be an ideal of R.
For
a, b 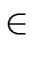 R the relation
R the relation
a - b 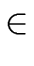 I I |
(12) |
usually denoted by
a  b mod I b mod I |
(13) |
defines an equivalence relation.
If we denote by
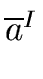 (or
(or
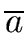 if not ambiguous)
the class of the element a,
then the residue classes of this relation forms a (commutative) ring (with unity)
denoted by R/I
where addition and multiplication are defined by
if not ambiguous)
the class of the element a,
then the residue classes of this relation forms a (commutative) ring (with unity)
denoted by R/I
where addition and multiplication are defined by
Proposition 3
Let R be an Euclidean domain and let a, m be in R.
Then
a mod m is a unit of R/m iff
gcd(a, m) = 1.
In this case the Extended Euclidean Algorithm can be used
to compute the inverse of
a mod m.
Proof.
Indeed, let
g be the gcd of
a and
m
and let
s,
t be the corresponding Bézout coefficients.
Hence we have
If
g = 1 then
s mod
m is the inverse of
a mod
m.
Conversly if
a mod
m is invertible there exists
b 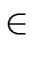 R
R such that
a b  1 mod m 1 mod m |
(20) |
That is there exists
c 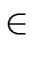 R
R such that
a b - 1 =
c m.
If
a and
m could be divided by an element
d
which is not a unit then we would be led to a contradiction
(
d (
a' b +
c m') = 1).
Hence
gcd(
a,
m) = 1.

Remark 4
The above remarks and proposition lead us to the following
ALDOR implementation of the residue class ring of an Euclidean
domain R by one of its element.
ResidueClassRing(R:EuclideanDomain, p:R): Ring with {
class: R -> %;
sample: % -> R;
} == R add {
Rep == R;
import from R;
1: % == per(1);
0: % == per(0);
zero?(x:%): Boolean == zero?(rep(x));
(x:%) = (y:%) : Boolean == zero?(x-y);
one?(x:%): Boolean == x = 1;
class(a:R):% == {
(q,r) := divide(a,p);
per(r);
}
sample(x:%): R == rep(x);
(x:%) + (y:%) : % == class(rep(x) + rep(y));
-(x:%) : % == class(-rep(x));
(x:%) * (y:%) : % == class(rep(x) * rep(y));
(n:Integer) * (x:%): % == class(n * rep(x));
(x:%) ^ (n:NonNegativeInteger) : % == class(rep(x) ^ n);
recip(x:%): Partial(%) == {
import from Partial(%);
(u,v,g) := extendedEuclidean(rep(x),p);
h?: Partial(R) := recip(g);
failed? h? => failed();
h: R := retract(h?);
[class(h * u)];
}
}
Proposition 4
Let
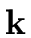
be a field and
f 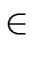
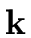
[
x]
with degree
n 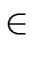

.
One arithmetic operation in the residue class ring
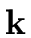
[
x]/
f,
that is, addition, multiplication or division by
an invertible element can be done using
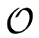
(
n2) arithmetic operations in
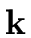
.
Explain why!
Theorem 1 (Fermat's little theorem)
If
p 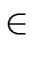

is a prime and
a 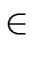
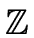
then we have
ap  a mod p a mod p |
(23) |
Moreover if
p does not divide
a then we have
ap-1 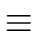
1 mod
p.
Proof.
It is sufficient to prove the claim for
a = 0
... p - 1
which we do by induction on
a.
The cases
a = 0 and
a = 1 are trivial.
For
a > 1 we have
ap = ((a - 1) + 1)p 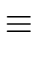 (a - 1)p + 1p (a - 1)p + 1p 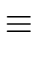 (a - 1) + 1 = a mod p (a - 1) + 1 = a mod p |
(24) |



Next: Modular Algorithms and interpolation
Up: The Euclidean Algorithm
Previous: The Extended Euclidean Algorithm
Marc Moreno Maza
2003-06-06
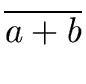 and
and  p | (qa - qb)p + ra - rb
p | (qa - qb)p + ra - rb  p | ra - rb
p | ra - rb ra = rb
ra = rb a(u) = b(u)
a(u) = b(u)