(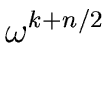 )2 = ( )2 = ( |
(53) |
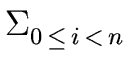 ai xi.
We define
ai xi.
We define
|
(51) |
| A(x) = A[0](x2) + x A[1](x2) | (52) |
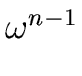 is reduced to evaluate A[0] and A[1] at
1,
is reduced to evaluate A[0] and A[1] at
1,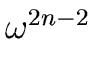 .
But this second sequence of values consists of two identical sequences
of length n/2.
Indeed for every integer k we have
.
But this second sequence of values consists of two identical sequences
of length n/2.
Indeed for every integer k we have
(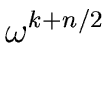 )2 = ( )2 = ( |
(53) |
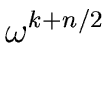 = - = - |
(54) |
1,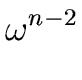 |
(55) |
1,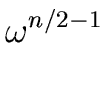 |
(56) |
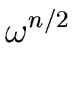 , ,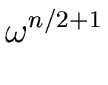 ,..., ,...,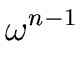 |
(57) |
-1, - 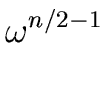 . . |
(58) |
The recursive calls of DFT(n, A,
THIS PART REQUIRES PROCESSING COMPLETELY BY HAND THE CASE n = 8.
THE FORMULA FOR t IN THE ABOVE ALGORITHM NEEDS TO BE CHECKED.
| 000, 001, 010, 011, 100, 101, 011, 111 | (59) |
| 000, 100, 010, 110, 001, 101, 110, 111 | (60) |
| f = f+ - f- and g = g+ - g- | (61) |
| f g = f+g+ + f-g- - f+g- - f-g+ | (62) |
| | ck | |
(63) |