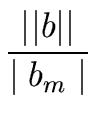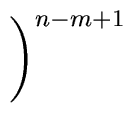Classical division with remainder

We assume that R is a commutative ring with unity. We consider the classical algorithm for univariate polynomial division with remainder stated over R instead of a field. However, Algorithm 5 is well defined because we assume that the leading coefficient of the polynomial b is a unit.

Algorithm 5  

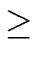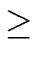
Proposition 5   Let a and b two univariate polynomials in R[x] with respective degrees n and m such that n $\geq$ m $\geq$ 0 and the leading coefficient of b is a unit. Then there exist unique polynomials q and r such that a = bq + r and deg r  <  m. The polynomials q and r are called the quotient and the remainder of a w.r.t. to b. 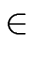Algorithm 5 compute them in (2m + 1)(n - m + 1) $\in$ $\cal {O}$(n m) operations in R.

Proof. We leave to the reader the proof of the uniqueness of the quotient and the remainder of a w.r.t. to b. So we focus now on the complexity result Consider an iteration of the for loop where deg r = m + i holds at the begining of the loop. Observe that r and q_ixⁱb have the same leading coefficient. Since deg b = m, computing the reductum of q_ixⁱb requires m operations. Then subtracting the reductum of q_ixⁱb to that of r requires again m operations. Hence each iteration of the for loop requires at most 2m + 1 operations in R, since we need also to count 1 for the computation of q_i. The number of for loops is n - m + 1. Therefore Algorithm 5 requires (2m + 1)(n - m + 1). $\qedsymbol$

Remark 10   One can derive from Algorithm 5 a bound for the coefficients of q and r, which is needed for performing a modular version (based for instance on the CRT). Let | | a | |, | | b | | and | | r | | be the max-norm of a, b and r. Let | b_m | be the absolute value (over $\mbox{${\mathbb Z}$}$) or the norm (over $\mbox{${\mathbb C}$}$) of the leading coefficient of b. Then we have

$$\leq \left(\vphantom{ 1 + \frac{{\mid}{\mid}b{\mid}{\mid}}{\mid b_m \mid} }\right. {\frac{{{\mid}{\mid}b{\mid}{\mid}}}{{\mid b_m \mid}}} \left.\vphantom{ 1 + \frac{{\mid}{\mid}b{\mid}{\mid}}{\mid b_m \mid} }\right)^{{n-m+1}}_{}$$ (64)