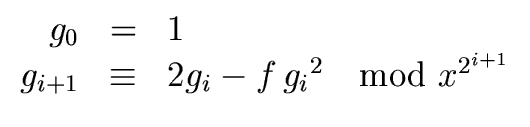Proof.
Indeed, let
g1 and
g2 be solutions of
Equation (
71).
Then the product
f (
g1 -
g2) is a multiple of
x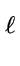
.
Since
f (0) = 1 then
g1(0) -
g2(0) must be 0.
Hence there is a constant
c 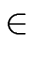 R
R and polynomials
h1,
h2
with degree less than
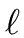
- 1 such that
| g1(x) = h1(x) x + c and g2(x) = h2(x) x + c |
(72) |
It follows that
f (
h1 -
h2) is a multiple of
x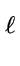 -1
-1.
By repeating the same argument we show that
h1(0) =
h2(0).
Then by induction on
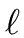
we obtain
g1 =
g2.

Theorem 9
Let
R be a commutative ring with unity.
Let
f be a polynomial in
R[
x] such that
f (0) = 1.
Let
g0,
g1,
g2,... be the sequence of polynomials defined
for all
i 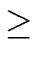
0 by
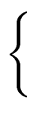 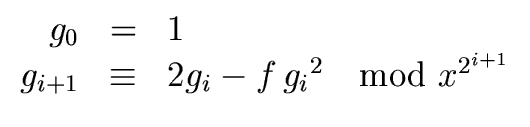 |
(75) |
Then for
i 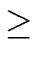
0 we have
f gi 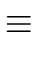 1 modx2i 1 modx2i |
(76) |
Proof.
Theorem
9
tell us that Algorithm
6
computes the inverse of
f modulo
x2r.
Since
x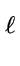
divides
x2r, the result is also valid modulo
x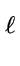
.
We do not give here a proof of the complexity result
and we refer to Theorem 9.4 in [
vzGG99].
In fact we prefer to give a very brutal explanation about it.
To understand the complexity result one needs to point out
the following relation for
i = 1 ... r.
gi 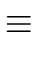 gi-1 modx2i-1 gi-1 modx2i-1 |
(79) |
Indeed, by virtue of
Theorem
9
we have
| gi |
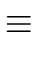 |
2gi-1 - f gi-12 |
modx2i |
| |
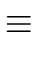 |
2gi-1 - f gi-12 |
modx2i-1 |
| |
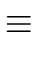 |
gi-1(2 - f gi-1) |
modx2i-1 |
| |
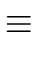 |
gi-1(2 - 1) |
modx2i-1 |
| |
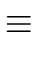 |
gi-1 |
modx2i-1 |
|
(80) |
Therefore when computing
gi we only to care about power of
x
in the range
x2i-1 ... x2i.
This says that
- half of the computation of gr is made
during the last iteration of the for loop,
- a quater is made when computing gr-1 etc.
Now recall that
So
roughly the cost of the algorithm is in the order
of magnitude of the cost of the last iteration.
which consists of
- two multiplications of polynomials with degree less than 2r,
- a multiplication of a polynomial (with degree less than 2r)
by a constant,
- truncations modulo x2r
- a subtraction of polynomials with degree less than 2r.
leading to
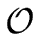
(
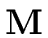
(2
r)) operations in
R.

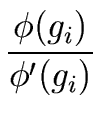
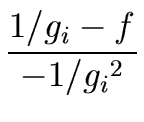 = 2gi - f gi2.
= 2gi - f gi2.