Proof.
Let
gr 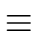 gr-1
gr-1 -
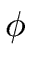
(
gr-1)
sr-1mod
p2r.
Then we have
g 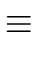 gr modp gr modp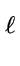 |
(124) |
In other words
gr is a
solution of higher precision.
Then proving the theorem turns into proving the invariants for
i = 0
... r
-
gi
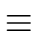 g0modp,
g0modp,
-
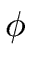 (gi)
(gi) 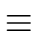 0 modp2i,
0 modp2i,
- if i < r then
si
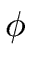
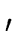 (gi)
(gi) 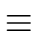 1 modp2i.
1 modp2i.
The case
i = 0 is clear and we assume that
i > 0 holds.
Then by induction hypothesis
p2i-1 divides
-
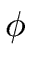 (gi-1)
(gi-1)
-
si-1 -
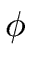
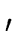 (gi-1)-1
(gi-1)-1
Then
p2i divides their product, that is
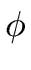 (gi-1si-1 (gi-1si-1 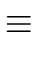 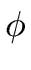 (gi-1) (gi-1)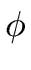 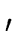 (gi-1)-1 modp2i. (gi-1)-1 modp2i. |
(125) |
Now we calculate
| gi |
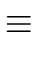 |
gi-1 - 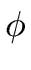 (gi-1)si-1 modp2i (gi-1)si-1 modp2i |
| |
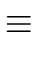 |
gi-1 - 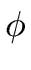 (gi-1) (gi-1)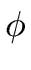 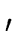 (gi-1)-1 modp2i (gi-1)-1 modp2i |
|
(126) |
Now applying Proposition
10
with
g =
gi,
h =
gi and
k = 2
i-1
we obtain the first two invariants.
...

![]()