

Next: Lucky and unlucky modular reductions
Up: Advanced Computer Algebra: The resultant
Previous: Relation between gcds in [x]
For univariate polynomials f, g over a field the following
lemma says that it is possible to find polynomials s, t
such that sf + tg,
deg(s) < deg(g),
deg(t) < deg(f )
if and only if
gcd(f, g) 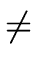 1.
1.
Lemma 1
Let
f,
g 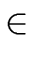
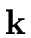
[
x] be nonzero polynomials
over the field
k.
Then the following statements are equivalent.
-
gcd(f, g)
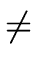 1
1
- There exist polynomials
s, t
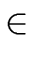 R[x]
R[x] 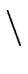 {0} such that
{0} such that
| sf + tg = 0, deg(s) < deg(g) and deg(t) < deg(f ) |
(24) |
Proof.
Let
h = gcd(
f,
g).
If
h 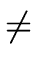
1 then
deg(
h)
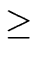
1 and a
solution is
| (s, t) = (g/h, - f /h) |
(25) |
Conversely, let (
s,
t) be a solution.
Assume that
f and
g are coprime.
Then
sf = -
tg would imply
f |
t.
This is impossible since
t 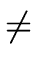
0 and
deg(
t) < deg(
f ).
Hence
f and
g are not coprime and
gcd(
f,
g)
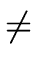
1 holds.

Proposition 4
Let
f,
g 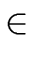
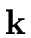
[
x] nonzero polynomials of degrees
n,
m such that
n +
m > 0.
Then we have:
-
gcd(f, g) = 1
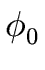 is an isomorphism.
is an isomorphism.
- If
gcd(f, g) = 1 then the Bézout coefficients (u, v)
computed by the Extended Euclidean Algorithm
form the unique solution in
Pm×Pn of the equation
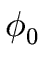 (u, v) = 1 (u, v) = 1 |
(29) |
Proof.
From Lemma
1 we deduce that
the kernel of
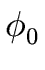
is reduced to {0} iff
gcd(
f,
g) = 1.
Since both
Pm×
Pn and
Pn+m have dimension
n +
m
this proves the first claim.
The second claim is a consequence of the first one.

Remark 8
Let's carry on with f, g nonzero univariate polynomials in x of degrees n, m
such that n + m > 0.
However let us relax the hypothesis on the coefficient ring
by assuming that it is just a commutative ring R with unity.
Let us write:
| f = fnxn + ... + f0 and g = gmxm + ... + g0 |
(30) |
The natural basis for
Pm×Pn consists
of the (xi, 0) for
0 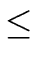 i < m followed by
the (0, xj) for
0
i < m followed by
the (0, xj) for
0 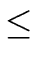 j < m.
On this basis
j < m.
On this basis 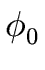 is represented by the following matrix
where all entries outside of the parallelograms
are equal to zero.
is represented by the following matrix
where all entries outside of the parallelograms
are equal to zero.
Definition 4
The above square matrix of order
n +
m is denoted
Sylv(
f,
g) and called
the
Sylvester matrix of
f and
g.
Its determinant is called the
resultant of
f and
g
denoted by
res(
f,
g).
We make the following conventions.
- If n = m = 0 (and still nonzero polynomials) we define
res(f, g) = 1.
- If f = 0 or
f
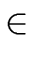 R[x]
R[x] 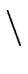 R then
res(f, 0) = res(0, f )= 0.
R then
res(f, 0) = res(0, f )= 0.
- If
f
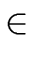 R
R 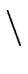 {0} then
res(f, 0) = res(0, f )= 1.
{0} then
res(f, 0) = res(0, f )= 1.
Proposition 5
Let
f,
g 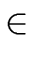
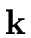
[
x] be nonzero univariate polynomials
over a field
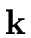
. Then the following statements are equivalent
-
gcd(f, g) = 1.
-
res(f, g)
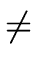 0.
0.
- there do not exist any
s, t
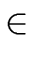
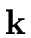 [x]
[x] 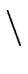 {0}
such that
{0}
such that
| sf + tg = 0, deg(s) < deg(g) and deg(t) < deg(f ). |
(32) |
Proof.
This follows from Proposition
4
and the fact that
res(
f,
g) is a determinant of the linear map
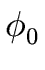
.

Proposition 6
Let
f,
g 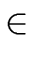 R
R[
x] be nonzero univariate polynomials
over a UFD
R. Then we have
gcd(f, g) 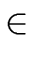 R R 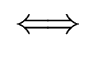 res(f, g) res(f, g) 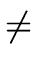 0. 0. |
(33) |
Proof.
This follows from the adaptation of the results of
Lemma
1
and Proposition
4
to the case where the ground ring is a UFD (and in particular
an integral domain) instead of a field.

Proposition 7
Let
f,
g 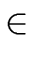 R
R[
x] be nonzero univariate polynomials
over an integral domain
R.
Then there exist nonzero
s,
t 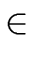 R
R[
x] such that
| sf + tg = res(f, g), deg(s) < deg(g) and deg(t) < deg(f ). |
(34) |
Proof.
Let
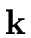
be the field of fractions of
R.
If
res(
f,
g) = 0 then we know that there exist
s,
t 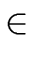
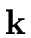
[
x]
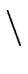
{0}
such that
| sf + tg = 0, deg(s) < deg(g) and deg(t) < deg(f ). |
(35) |
Then the claim follows by cleaning up the denominators.
If
res(f, g) 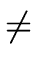 0 then f and g are coprime
in
0 then f and g are coprime
in
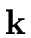 [x].
Then there exists
u, v
[x].
Then there exists
u, v 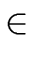
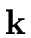 [x] with stated degree bounds
such that
uf + vg = 1 holds in
[x] with stated degree bounds
such that
uf + vg = 1 holds in
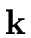 [x].
Observe that
[x].
Observe that
- The coefficients of u, v are in fact the unique
solution of a linear system whose matrix is the
Sylvester
Sylv(f, g) matrix of f and g.
- These coefficients can be computed by the
Cramer's rule.
- Hence each of these coefficients is the
quotient of a determinant of a submatrix of
Sylv(f, g)
by
res(f, g).
Then the polynomials
s =
res(
f,
g)
u and
t =
res(
f,
g)
u
have coefficients in
R and we have the desired relations.



Next: Lucky and unlucky modular reductions
Up: Advanced Computer Algebra: The resultant
Previous: Relation between gcds in [x]
Marc Moreno Maza
2003-06-06
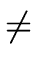 1
1
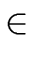 R[x]
R[x]  {0} such that
{0} such that
![$\displaystyle \begin{array}{lll} {\bf k}[x] \times {\bf k}[x] & \rightarrow & {\bf k}[x] \\ (s,t) & \longmapsto & s f + tg \\ \end{array}$](img32.png)
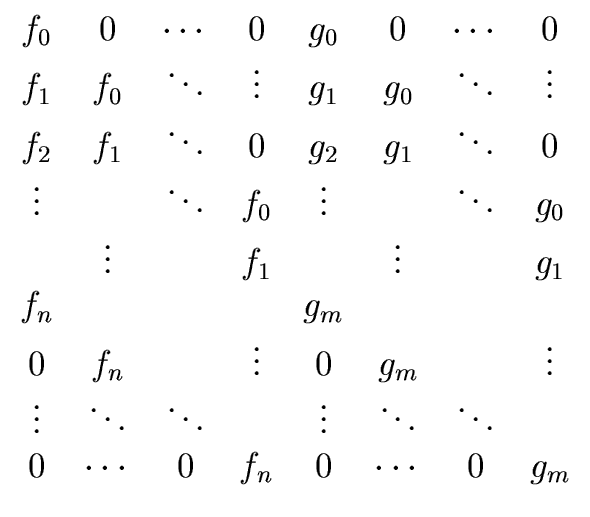
 res(f, g)
res(f, g) ![]() 0 then f and g are coprime
in
0 then f and g are coprime
in
![]() [x].
Then there exists
u, v
[x].
Then there exists
u, v ![]()
![]() [x] with stated degree bounds
such that
uf + vg = 1 holds in
[x] with stated degree bounds
such that
uf + vg = 1 holds in
![]() [x].
Observe that
[x].
Observe that