Let us recall that an element a ![]() R
R
![]() 0
0
![]() R
R
![]() 0
0
Let us recall also that because the ring R
|
(1) |
Observe also the ring R
![]()
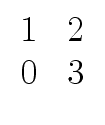
![]()
Why do we need to take such exotic examples?
Because among the rings you are familiar with, this is
the simplest example of ring having zero divisors, units
and nonzero elements that are not zero divisors or units.
Indeed our usual rings are
![]() [x]
[x]
![]()
![]() /m
/m![]()
![]() [x]
[x]
![]() /m
/m![]()
![]() /m
/m![]()
![]() /6
/6![]() [x]
[x]
| a = g a' and m = g m' | (3) |
| m' a = m' g a' = m a' |
(4) |
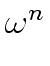 = 1
= 1
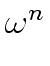 = 1
= 1
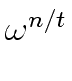 - 1
- 1
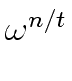
(1) -> R := PF(17)
(1) PrimeField 17
Type: Domain
(2) -> w: R := 3
(2) 3
Type: PrimeField 17
(3) -> [w^i for i in 0..16]
(3) [1,3,9,10,13,5,15,11,16,14,8,7,4,12,2,6,1]
Type: List PrimeField 17
(4) -> u: R := 2
(4) 2
Type: PrimeField 17
(5) -> [u^i for i in 0..16]
(5) [1,2,4,8,16,15,13,9,1,2,4,8,16,15,13,9,1]
Type: List PrimeField 17
The first list shows that 3
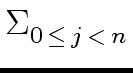
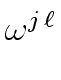 = 0
= 0
Let us prove the first statement of the lemma.
Let g
Now let us prove the second statement of the lemma.
By applying Relation (5)
with
c = ![]()
![]()
![]()
Since
![]() < n
< n
![]() g < n
g < n
g | (n/t)
(7)
Let
c =
![]() and m = n/(tg)
and m = n/(tg)
(8)
in Relation (5) leading to
(
![]() -1) a = (
-1) a = (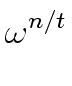 - 1)
- 1)
(9)
for some a ![]() R
R
![]() - 1)
- 1)
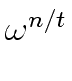 - 1)
- 1)
![]()
![]() - 1)
- 1)
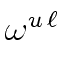 - 1)
- 1)
(
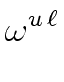 -1) = (
-1) = (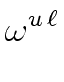
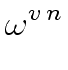 -1) = (
-1) = (![]() - 1)
- 1)
(10)
Hence
(
![]() -1) | (
-1) | (![]() - 1)
- 1)
(11)
Therefore
(![]() - 1)
- 1)
![]()
(
![]() -1)
-1) 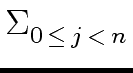
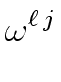 =
= 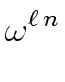 -1 = 0
-1 = 0
(12)
Since
(![]() - 1)
- 1)
![]()