mathend000#-th root of unity,
Let us consider the product of the matrix
V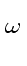 mathend000# and
V
mathend000# and
V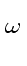
 mathend000#.
The element at row i
mathend000# and column k
mathend000# is
mathend000#.
The element at row i
mathend000# and column k
mathend000# is
(V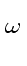 V V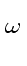 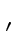 )ik )ik |
= |
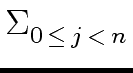 (V (V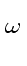 )ij(V )ij(V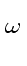 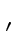 )jk )jk |
| |
= |
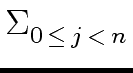 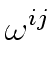 ( (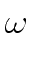 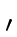 )jk )jk |
| |
= |
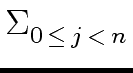 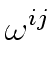 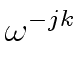 |
| |
= |
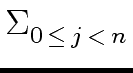 ( (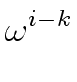 )j )j |
|
(16) |
Observe that
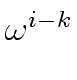 mathend000# is either a power of
mathend000# is either a power of 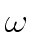 mathend000# or a power of its inverse.
Thus, in any case this is a power of
mathend000# or a power of its inverse.
Thus, in any case this is a power of 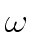 mathend000#.
If i = k
mathend000# this power is 1
mathend000# and
(V
mathend000#.
If i = k
mathend000# this power is 1
mathend000# and
(V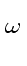 V
V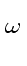
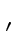 )ik
mathend000# is equal to n
mathend000#.
If i
)ik
mathend000# is equal to n
mathend000#.
If i 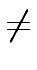 k
mathend000# then the conclusion follows by applying the second statement of
Lemma 1
which shows that
(V
k
mathend000# then the conclusion follows by applying the second statement of
Lemma 1
which shows that
(V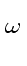 V
V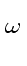
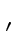 )ik = 0
mathend000#.
)ik = 0
mathend000#.

![]()
![]() R
R
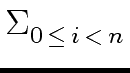 fi xi
fi xi 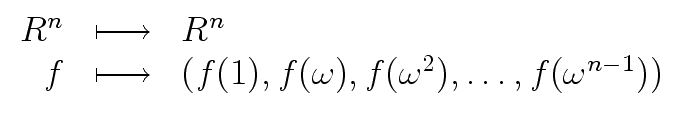
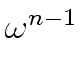 )
)
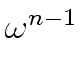 )
)
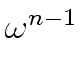
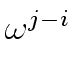 ) = 0
) = 0
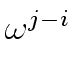 )
)
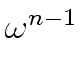
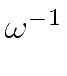
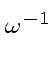 = nIn
= nIn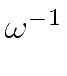
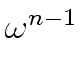
![]()
![]()
![]()
![]() V
V![]()
![]() )ik
)ik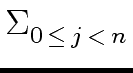 (V
(V![]() )ij(V
)ij(V![]()
![]() )jk
)jk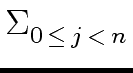
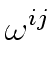 (
(![]()
![]() )jk
)jk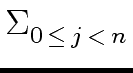
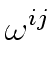
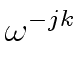
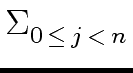 (
(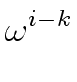 )j
)j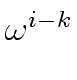
![]()
![]()
![]() V
V![]()
![]() )ik
)ik
![]() k
k
![]() V
V![]()
![]() )ik = 0
)ik = 0
![]()