

Next: Syntax Trees for Expressions
Up: Compiler Theory: Syntax-Directed Translation
Previous: Compiler Theory: Syntax-Directed Translation
A SYNTAX-DIRECTED DEFINITION is a context-free grammar in which
It is usual to denote the attributes of a grammar symbol
in the form X.name where name is an meaningful name for the attribute.
Example 1
The following syntax-directed definition generates binary strings
where (one of) the attributes gives the number represented by the
string. The nonterminals are B and D, the terminals are 0 and 1.
The symbol B stands for binary expansion and the symbol D
stands for digit.
|
Grammar symbol |
Synthesized attribute |
Inherited attribute |
|
B |
B.pos, B.val |
|
|
D |
D.val |
D.pow |
|
Production |
Semantic Rule |
B  DB1 DB1 |
B.pos :=
B1.pos + 1 |
|
B.val :=
B1.val + D.val |
|
D.pow := B1.pos |
B  D D |
B.pos := 1 |
|
B.val := D.val |
|
D.pow := 0 |
D  0 0 |
D.val := 0 |
D  1 1 |
D.val := 2D.pow |
AT A PARSE TREE NODE, following the previous definition,
- the value of a synthesized attribute is computed
from the values of the attributes of the children of the node.
- the value of an inherited attributes is computed
from the values of the attributes of its siblings
(brothers and sisters) and parents.
Example 2
Let us continue Example 1
and let us consider the input string w = 1010.
Figure 1 shows a parse
tree for w.
Figure 1:
Parse tree for w = 1010.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree2.eps}
\end{figure}](img4.png) |
Figure 2 shows the values
of the attributes at each node.
Figure 2:
Annotated parse tree for w = 1010.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree2b.eps}
\end{figure}](img5.png) |
|
Production |
Semantic Rule |
B  DB1 DB1 |
B.pos :=
B1.pos + 1 |
|
B.val :=
B1.val + D.val |
|
D.pow := B1.pos |
B  D D |
B.pos := 1 |
|
B.val := D.val |
|
D.pow := 0 |
D  0 0 |
D.val := 0 |
D  1 1 |
D.val := 2D.pow |
SEMANTIC RULES set up dependencies between attributes that will be represented
as a dependency graph.
- From this dependency graph, we will derive an evaluation order
for the semantic rules.
- This evaluation order defines the values of the attributes at the
nodes in a parse tree.
- Terminals do not have semantic rules since their attributes are
supplied by the lexical analyzer.
ATTRIBUTE GRAMMARS. It is useful to allow side effects (printing a value, updating
a global variable, ...) in semantic rules.
Such semantic rules are written as procedure calls or program fragments like
However these semantic rules can be thought of as rules defining the values
of dummy attributes.
An attribute grammar is a syntax-directed definition
where the semantic rules cannot have side effects.
A S-ATTRIBUTE GRAMMAR is an attribute grammar where all attributes are synthesized
attributes.
The interest of an S-attribute grammar is that
any parse tree can always be annotated by evaluating
the semantic rules for the attributes at each node
bottom up, from the leaves to the root.
AN ANNOTATED PARSE TREE. is a parse tree showing the values of the attributes
at each node.
The process of computing the attribute values
at the nodes is called annotating or decorating
the parse tree.
Example 4
The following syntax-directed definition implements statements for declaring
identifiers  with type
with type
 and
and 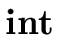 .
Note that the comma , is also a terminal symbol for this grammar.
The addtype procedure is used to add the type of an identifier
in the symbol table (by accessing its entry in the symbol table with
.
Note that the comma , is also a terminal symbol for this grammar.
The addtype procedure is used to add the type of an identifier
in the symbol table (by accessing its entry in the symbol table with
 .entry).
.entry).
|
Grammar symbol |
Synthesized attribute |
Inherited attribute |
|
L |
|
L.in (string) |
|
T |
T.type (string) |
|
 |
 .entry .entry 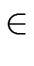 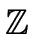 |
|
|
Production |
Semantic Rule |
D  TL TL |
L.in := T.type |
T  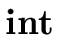 |
T.type := 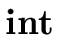 |
T   |
T.type :=
 |
L  L1 L1  |
L1.in := L.in |
|
addtype
( .entry, L.in) .entry, L.in) |
L   |
addtype
( .entry, L.in) .entry, L.in) |
- The nonterminal T has a synthesized attribute whose value
is received by the inherited attribute of L via the semantic rule L.in := T.type.
- Then the type L.in is passed down a parse tree via the semantic rule
L1.in := L.in.
Figure 3:
Parse tree for
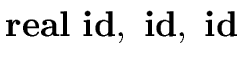 .
.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1.eps}
\end{figure}](img15.png) |
Remark 1
To compute the values of the attributes at each node
of an annotated parse tree we need to define
an evaluation order.
This will be done by a dependency graph.
DEPENDENCY GRAPH. Let us a consider a syntax-directed definition.
Let us assume that every semantic rule as the form
Let T be an annotated tree for this syntax-directed definition.
Let N be an internal node of T and let
A 
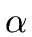 be the associated production.
Let b :=
f (c1,..., ck) be a semantic rule associated
with this production.
Then for
i = 1 ... k we say that
the attribute b depends on the attribute ci.
be the associated production.
Let b :=
f (c1,..., ck) be a semantic rule associated
with this production.
Then for
i = 1 ... k we say that
the attribute b depends on the attribute ci.
Let 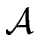 be the set of all attributes.
The underlying idea guiding the construction of
the dependency graph of T is: if an attribute b the node N
of T depends on the attribute ci then ci must before
evaluated before b.
Thus, it is tempting to consider the graph of the relation
be the set of all attributes.
The underlying idea guiding the construction of
the dependency graph of T is: if an attribute b the node N
of T depends on the attribute ci then ci must before
evaluated before b.
Thus, it is tempting to consider the graph of the relation
(b, c) 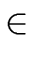 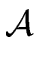 × ×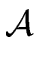  b depends on c b depends on c |
(4) |
However a given grammar symbol X may label different nodes of T.
Therefore the dependency graph of T
is the directed graph constructed as follows.
Algorithm 1
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] An annota...
...{\sf create} an arc from $Z.c(P)$\ to $Y.b(M)$\ \\
\end{tabbing}\end{minipage}}](img20.png)
Given a node N of the annotated tree T labeled by the grammar symbol X
it is convenient to call attribute of N every attribute of X.
Example 5
Figure 4:
Parse tree for
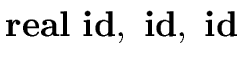 with dummy synthesized attributes.
with dummy synthesized attributes.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1b.eps}
\end{figure}](img21.png) |
Figure 5:
Parse tree for
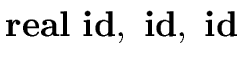 with dummy synthesized attributes and
showing the attributes of each mode.
with dummy synthesized attributes and
showing the attributes of each mode.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1c.eps}
\end{figure}](img22.png) |
Figure 6:
Construction of the vertices of the dependency graph.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1d.eps}
\end{figure}](img23.png) |
Figure 7:
Construction of the arcs of the dependency graph.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1e.eps}
\end{figure}](img24.png) |
Figures 4, 5,
6 and 7
show the construction of the vertices and the arcs of the
dependency graph G of the parse tree of Figure 3.
Observations.
- This graph has 10 vertices (shown on Figures 6
and 7 by rectangles with corners made round.
- The arcs of G are shown on Figure 7.
- An arc in the parse tree does not become necessarily an arc in the
dependency graph.
- The dependency graph G has no circuits (or even cycles).
DIRECTED GRAPHS. let G be a directed graph with vertex set X
and arc set A.
The following definitions are very useful.
- A path in G is a sequence of vertices
(x1, x2,..., xn) such that
for every
i = 1 ... n - 1 the couple
(xi, xi+1) is an arc of G.
- A circuit in G is a path
(x1, x2,..., xn) such that
x1 = xn.
- A chain in G is a sequence of vertices
(x1, x2,..., xn) such that
for every
i = 1 ... n - 1 either the couple
(xi, xi+1) or
the couple
(xi+1, xi) is an arc of G.
- A cycle in G is a chain
(x1, x2,..., xn) such that
x1 = xn.
- A directed graph is said acyclic if it has no cycles.
Such a graph is also called a DAG.
SOURCES IN DIRECTED GRAPHS. A source in the directed graph G is a vertex x
such that for every other vertex y the couple (y, x) is not an arc.
In broad words, there is no path leading to a source.
It is not hard to see that every DAG has at least one source.
(Otherwise there would be a circuit and thus a cycle).
TOPOLOGICAL SORT OF A DAG. Let
G = (X, A) be a DAG with n vertices.
A topological sort of the DAG G is
an enumeration of its vertices (a bijection
from
{1,..., n} to X) say
x1, x2,..., xn such that
there is no path from xj to xi for
1 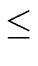 i < j
i < j 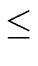 n.
n.
By induction on n, it is not hard to see that
every DAG has a topological sort.
Indeed, the case n = 1 is trivial.
For n > 1 let s be a source of G.
Let G - s be the graph induced from G by the cancellation
of s and every arc leaving from s.
By the induction hypothesis, the graph G - s has
a topological sort, say
x1, x2,..., xn-1.
Now observe that
s, x1, x2,..., xn-1
is a topological sort of G.
THE TRANSITIVE CLOSURE OF A DIRECTED GRAPH
- The directed graph G is transitive if for every vertex
x, y, z such that (x, y) and (y, z) are arcs of G
then (x, z) is also an arc of G.
- The transitive closure
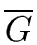 of the directed graph
G = (X, A) is the smallest graph (by its
arc set) which is transitive and for which
G is a subgraph.
In other words, the graph
of the directed graph
G = (X, A) is the smallest graph (by its
arc set) which is transitive and for which
G is a subgraph.
In other words, the graph
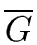 is such that
is such that
-
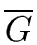 is transitive,
is transitive,
- every arc of G is an arc of
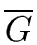 ,
,
- and
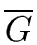 is the smallest graph with these properties.
is the smallest graph with these properties.
- Observe that for that two vertices x, y of G
the couple (x, y) is an arc of
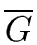 iff
there is a path from x to y.
iff
there is a path from x to y.
- Therefore the knowledge of
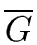 allow us to answer
the following questions.
allow us to answer
the following questions.
- Does G possess a circuit? If yes, a topological sort
can be constructed.
- Is
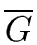 antisymmetric? If both G and
antisymmetric? If both G and
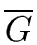 have no loops (arcs of the form (x, x)) then
have no loops (arcs of the form (x, x)) then
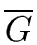 is antisymmetric.
Hence
is antisymmetric.
Hence
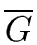 is the graph of a pre-ordering
(that is a relation on the vertices which is antisymmetric
and transitive).
Then a sort algorithm (heap-sort, quick-sort, merge-sort)
can be applied to sort the veritces of
is the graph of a pre-ordering
(that is a relation on the vertices which is antisymmetric
and transitive).
Then a sort algorithm (heap-sort, quick-sort, merge-sort)
can be applied to sort the veritces of
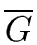 .
This gives a topological sort for G.
.
This gives a topological sort for G.
COMPUTING THE TRANSITIVE CLOSURE OF A DIRECTED GRAPH
- There are many techniques to compute
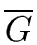 .
For instance we can compute the shortest length of a path
between every couple of vertices.
We describe now how to do this.
.
For instance we can compute the shortest length of a path
between every couple of vertices.
We describe now how to do this.
- Let G be a directed graph with n vertices
that we denote by
1, 2,..., n.
- To every couple (i, j) of G we associate
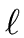 (i, j)
(i, j) 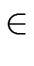
 the length of the arc (i, j), if (i, j) is an arc of G,
and
+
the length of the arc (i, j), if (i, j) is an arc of G,
and
+ 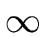 otherwise.
otherwise.
- Then to every couple (i, j) we associate L(i, j) the length
of the shortest path from i to j, if any, and
+
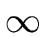 otherwise.
otherwise.
- Let k, i, j be integers in the range
1 ... n.
We call k-path from i to j a path using intermediate vertices
(excluding i and j) in the range
1 ... k.
Let
L(k)(i, j) be the length of the shortest k-path from i to j.
We define
L(0)(i, j) =
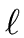 (i, j).
(i, j).
- Then
L(n)(i, j) = L(i, j). Moreover the matrices
L(1), L(2),..., L(n) can be computed iteratively
by using the following relation for every
k = 1 ... n
| L(k)(i, j) = min(L(k-1)(i, j), L(k-1)(i, k) + L(k-1)(k, j)) |
(5) |
Indeed a shortest k-path from i to j is
- either a shortest (k - 1)-path from i to j,
- or a shortest (k - 1)-path from i to k followed
by a shortest (k - 1)-path from k to j.
- This leads to Algorithm 2.
Algorithm 2
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] A directe...
...k) + L^{(k-1)}(k,j)).$\ \\
\> {\bf return} $L^(n).$\end{tabbing}\end{minipage}}](img30.png)
COMPUTING A TOPOLOGICAL SORT OF A DAG. In our simple example we obtain a topological sort
easily by canceling the sources one after another.
This leads to Figure 8.
Figure 8:
Topological sort for the dependency graph.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1f.eps}
\end{figure}](img31.png) |
Coming back to the parse tree (where the nodes without
attributes are removed, for clarity) we obtain
an order for evaluating the attributes.
This leads to the annotated parse tree
on Figure 9
where the order for executing the semantic rules
is shown by increasing numbers.
Figure 9:
Annotated parse tree (where nodes without attributes are removed).
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1g.eps}
\end{figure}](img32.png) |
Let us denote by ai the attribute associated with the
i-th node in the topological sort of the dependency graph.
We finally obtain the following program.
a4 :=
 |
| a5 := a4 |
| a7 := a5 |
addtype
(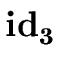 .entry, a5) .entry, a5) |
| a9 := a7 |
addtype
(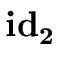 .entry, a7) .entry, a7) |
addtype
(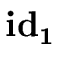 .entry, a9) .entry, a9) |
Remark 2
A grammar which is suitable for parsing (as the one of the
detailed Example 4)
may not be suitable for translation (i.e. may lead to an expensive
translation scheme).
In the following example, which also implements statements for declaring
identifiers, inherited attributes are avoided.
Thus the construction of a dependency graph is not needed.
|
Production |
Semantic Rule |
D  L L |
|
T  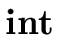 |
T.type := 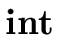 |
T   |
T.type :=
 |
L   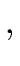 L1 L1 |
L.type := L1.type |
|
addtype
( .entry, L1.type) .entry, L1.type) |
L  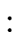 T T |
L.type := T.type |
Example 6
The following syntax-directed definition implements statements for
performing substitutions.
|
Grammar symbol |
Synthesized attribute |
Inherited attribute |
|
S |
|
|
|
E |
E.val 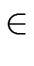  |
E.env |
- The attribute E.val is an integer value
- The attribute E.env is a list of bindings where
a binding is a pair (
 , value).
Hence E.env is a symbol table.
, value).
Hence E.env is a symbol table.
There are three functions used in the semantic rules.
- initialEnv
- which returns the empty environment.
- LookUp
- which determines the value of an identifier by consulting
the environment.
- Update
- which adds a binding to the environment.
In the above syntax-directed definition E1, E2 and E3 correspond to the
same nonterminal E.
|
Production |
Semantic Rule |
S  E E |
E.env := initialEnv() |
E1    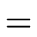 E2 E2 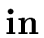 E3 E3 
|
E2.env := E1.env |
|
E3.env := Update(
E1.env, , E2.val) , E2.val) |
|
E1.val := E3.val |
E1  (E2 + E3) (E2 + E3) |
E1.val :=
E2.val + E3.val |
|
E2.env := E1.env |
|
E3.env := E1.env |
E   |
E.val := LookUp(
 , E.env) , E.env) |
E  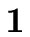 |
E.val := 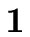 |
E  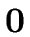 |
E.val := 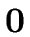 |
CONCLUSIONS
- We have provided a general method for evaluating
semantic rules.
- To build an annotated tree with n nodes in its dependency graph
the cost is
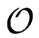 (n3).
(n3).
- We aim to reduce this cost by several ad-hoc techniques in the next
sections.


Next: Syntax Trees for Expressions
Up: Compiler Theory: Syntax-Directed Translation
Previous: Compiler Theory: Syntax-Directed Translation
Marc Moreno Maza
2004-12-02
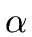 or A,
or A,
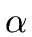 and the values
c1,..., ck
are attributes of the grammar symbols of
and the values
c1,..., ck
are attributes of the grammar symbols of 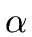 or A.
or A.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree2.eps}
\end{figure}](img4.png)
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree2b.eps}
\end{figure}](img5.png)
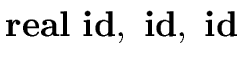 .
.![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1.eps}
\end{figure}](img15.png)
 b depends on c
b depends on c![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] An annota...
...{\sf create} an arc from $Z.c(P)$\ to $Y.b(M)$\ \\
\end{tabbing}\end{minipage}}](img20.png)
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1b.eps}
\end{figure}](img21.png)
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1c.eps}
\end{figure}](img22.png)
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1d.eps}
\end{figure}](img23.png)
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1e.eps}
\end{figure}](img24.png)
![\fbox{
\begin{minipage}{12 cm}
\begin{description}
\item[{\bf Input:}] A directe...
...k) + L^{(k-1)}(k,j)).$\ \\
\> {\bf return} $L^(n).$\end{tabbing}\end{minipage}}](img30.png)
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1f.eps}
\end{figure}](img31.png)
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.35]{annotatedParseTree1g.eps}
\end{figure}](img32.png)
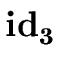 .entry, a5)
.entry, a5)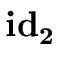 .entry, a7)
.entry, a7)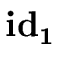 .entry, a9)
.entry, a9)