

Next: Translation Schemes
Up: Compiler Theory: Syntax-Directed Translation
Previous: Syntax-Directed Definitions
In this section, we consider the case where
- the input language consists of arithmetic expressions
(in a general sense that we will make precise below)
like arithmetic expressions in the usual sense,
or regular expressions, or S-expressions, etc.
- the output intermediate representation for an input sentence is a tree
reflecting the syntax structure of the sentence.
In this case,
- we will forbid inherited attributes,
- we will simplify the constructions of the parse tree and the annotated tree,
- and we will avoid the construction of the dependency graph.
ARITHMETIC EXPRESSIONS. A language L over an alphabet 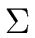 is
a language of arithmetic expressions (or expressions for short)
if there exists
is
a language of arithmetic expressions (or expressions for short)
if there exists
- a partition
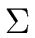 =
= 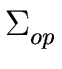
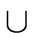
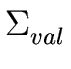
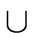 {
{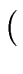 ,
,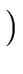 },
},
- a grammar G generating L such that each production has one of the forms
-
A
 a for
a
a for
a 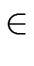
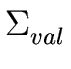
-
A
 (B)
(B)
-
A

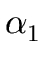
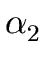 ,...
,...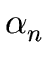 where n
where n 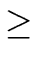 2 and where the
2 and where the
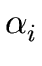 's are grammar symbols and
such that at most one of them belongs to
's are grammar symbols and
such that at most one of them belongs to
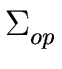 , the other symbols being nonterminals.
, the other symbols being nonterminals.
The elements of
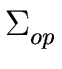 are called operators
and those of
are called operators
and those of
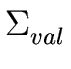 are called values.
The nonterminals on the right side of a production where an operator
appears are called operands of the production.
are called values.
The nonterminals on the right side of a production where an operator
appears are called operands of the production.
The language L is said
- binary infix if every production has the form
A
 a for
a
a for
a 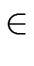
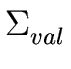 ,
A
,
A  (B) or
A
(B) or
A  BfC where
f
BfC where
f 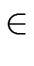
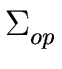 .
.
- binary postfix if every production has the form
A
 a for
a
a for
a 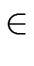
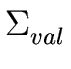 ,
A
,
A  (B) or
A
(B) or
A  BCf where
f
BCf where
f 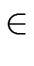
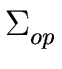 .
.
- binary prefix if every production has the form
A
 a for
a
a for
a 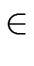
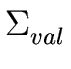 ,
A
,
A  (B) or
A
(B) or
A  fBC where
f
fBC where
f 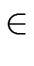
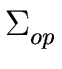 .
.
KEY IDEAS.
- The first idea is to condense the double construction
parse tree + annotated tree
in a single construction.
For arithmetic expressions this is quite easy as we shall see
- The second idea is to avoid the duplications of nodes
that stand for two (syntactically) equal subexpressions.
For (arithmetic) expressions this is again quite easy
by using dags.
CONSTRUCTING SYNTAX TREES FOR EXPRESSIONS. Each node in a syntax tree for an (arithmetic) expression
is a record with several fields.
- In the node for an operator, one field identifies
the operator and the remaining fields contain pointers
to the nodes of the operands.
The operator is often called the label of the node.
- In the leaf for an identifier, one field (the label) indicates
that this is an identifier and another field is a pointer
to the symbol-table entry for this identifier.
- In the leaf for a value, one field (the label) indicates
that this is a value (may be this field gives the type
of the value) and another field is the value
(or a pointer to this value).
We use here the following functions to create the nodes
of syntax trees for expressions with binary operators.
Each function returns a pointer to a newly created node.
- make_node
- (op, left, right) creates an
operator node with label op and two fields containing
pointers to left and right.
- make_leaf
- (
 , entry) creates an identifier
leaf with label
, entry) creates an identifier
leaf with label  and a field containing entry
a pointer to the symbol-table entry for the identifier.
and a field containing entry
a pointer to the symbol-table entry for the identifier.
- make_leaf
- (
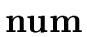 , val) creates a number leaf
with label
, val) creates a number leaf
with label 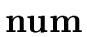 and a field containing val.
and a field containing val.
Example 7
The following syntax-directed definition allows the construction
of a syntax tree for a binary infix arithmetic expression.
The synthesized attributes E.ptr, T.ptr and F.ptr
keep track of the pointers returned by the function calls.
|
Production |
Semantic Rule |
E  E1 + T E1 + T |
E.ptr := make_node(
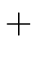 , E1.ptr, T.ptr) , E1.ptr, T.ptr) |
E  E1 - T E1 - T |
E.ptr := make_node(
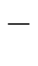 , E1.ptr, T.ptr) , E1.ptr, T.ptr) |
E  T T |
E.ptr := T.ptr |
T  T1*F T1*F |
T.ptr := make_node(
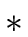 , T1.ptr, F.ptr) , T1.ptr, F.ptr) |
T  F F |
T.ptr := F.ptr |
F  (E) (E) |
F.ptr := E.ptr |
F   |
F.ptr := make_leaf( , ,
 .entry) .entry) |
F  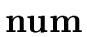 |
F.ptr := make_leaf(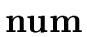 , ,
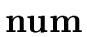 .val) .val) |
USING DAGS FOR SYNTAX TREES OF EXPRESSIONS.
- A dag for an expression identifies the common subexpressions
in the expression.
- Like a syntax tree, a dag has a node for every subexpression
of the expression.
- The difference is that a node in a dag representing a common
subexpression has more than one parent.
- Thus, before constructing a node with label op and fields with pointers
to left and right, the operation
make_node(op, left, right) checks if such a node
has already been constructed.
Figure 10:
A dag for the expression
a + a*(b - c) + (b - c)*d.
![\begin{figure}\htmlimage
\centering\includegraphics[scale=.4]{dagForArithmeticSubexpression.eps}
\end{figure}](img59.png) |
IMPLEMENTING DAGS FOR SYNTAX TREES OF EXPRESSIONS.
- To construct dags for expressions in an efficient manner
one could use an array of records.
- To avoid (explicit) pointers we can refer to a node
by its index (or position) in this array of records.
- Each record implements a node (or leaf).
For an operator node this record will contain
- the label of the operator,
- the indices of the children.
- This kind of representations allows search for existing subexpressions in linear
time.
- This can be improved by using hash-tables.
- A hash-table will be in our case an array of buckets where
a bucket is a linked list of nodes (each node being represented by
a record as in the previous data structure).
- We assume that we are given a hash-function h which converts
a label into a non-negative machine integer.
- To perform make_node(op, left, right) we first
compute h(op) which returns the bucket number in
which to search the node (and may be store the node if not yet present).
- In practice we expect each bucket to contain a small number of nodes.
- If
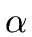 is the expected maximum length of a bucket, then
search/insertion of nodes can be done in
is the expected maximum length of a bucket, then
search/insertion of nodes can be done in
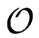 (
(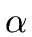 )
rather than in
)
rather than in
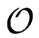 (n) where n is the number of nodes
currently stored.
(n) where n is the number of nodes
currently stored.


Next: Translation Schemes
Up: Compiler Theory: Syntax-Directed Translation
Previous: Syntax-Directed Definitions
Marc Moreno Maza
2004-12-02
![]() is
a language of arithmetic expressions (or expressions for short)
if there exists
is
a language of arithmetic expressions (or expressions for short)
if there exists
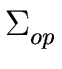
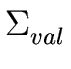
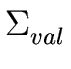
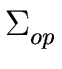 , the other symbols being nonterminals.
, the other symbols being nonterminals.
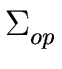 are called operators
and those of
are called operators
and those of
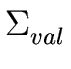 are called values.
The nonterminals on the right side of a production where an operator
appears are called operands of the production.
are called values.
The nonterminals on the right side of a production where an operator
appears are called operands of the production.
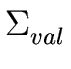 ,
A
,
A 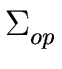 .
.
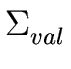 ,
A
,
A 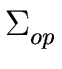 .
.
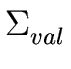 ,
A
,
A 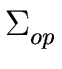 .
.