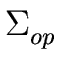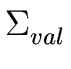Translation Schemes

In this section, we enhance the notion of a syntax-directed definitions in order to specify the order of evaluation of the semantic rules, leading to the concept of a translation scheme.

KEY FEATURES.

• For each sentence of the underlying grammar, a parse tree (decorated with attributes and semantic rules) is constructed.
• But a dependency graph is not computed.

Translation schemes are well adapted when the semantic rules are procedure calls.

A TRANSLATION SCHEME is a context-free grammar in which semantic rules are embedded within the right sides of the productions.

• So a translation scheme is like a syntax-directed definition, except that the order of evaluation of the semantic rules is explicitly shown.
• The position at which an action is to be executed
  • is shown by enclosing it between braces
  • and writing it within the right side of the production.
• When drawing a parse tree for a translation scheme, an action is indicated by constructing an extra child, connected by a dashed line to the node of the production.
• The order in which the actions are executed is the order in which they appear during a depth-first traversal of a parse tree.

Example 8   Let L be a language of arithmetic expressions over the alphabet

$$\Sigma \Sigma_{{{op}}}^{{}} \cup \Sigma_{{{val}}}^{{}} \cup \bf ( \bf )$$ (6)

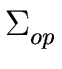where $\Sigma_{{{op}}}^{{}}$ is the set of operators and 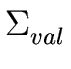$\Sigma_{{{val}}}^{{}}$ the set of values. We assume that L is binary infix. We associate to L a language L' of arithmetic expressions, binary postfix. This is given by a map p defines as follows.

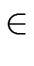
• for a 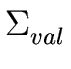$\in$ $\Sigma_{{{val}}}^{{}}$ we have p(a) = a
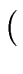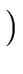• for nonterminals B we have p( $\bf ($B$\bf )$ ) = B.
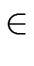
• for nonterminals B, C and f 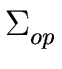$\in$ $\Sigma_{{{op}}}^{{}}$ we have p(B f C) = B C f.

The translation from L to L' can be made by a syntax-directed definition of the form

Production	Semantic Rule
A $\longmapsto$ a	A.str := a
A $\longmapsto$ (B)	A.str := B.str
A $\longmapsto$ B f C	A.str := concat(B.str, C.str, " f")

where A.str, B.str and C.str are synthesized attributes of type string and where concat is a concatenation function for strings. Since this syntax-directed definition has no inherited attributes, the evaluation of the attributes (and consequently the translation) will be easy. However, observe that for a large expression, a certain amount of time and space will be needed to create all the attributes.

It is possible to speed up translations from L to L' by considering the following translation scheme.

A	$\longmapsto$	a { output(a) }
A	$\longmapsto$	(B) { }
A	$\longmapsto$	B f C { output(f) }

We illustrate the notions of syntax tree and translation scheme with the expression a + (a + d )*(b - c).

• Figure 11 shows a syntax tree for this expression. Observe that there is no need to show parenthesis on a syntax tree since there is no ambiguity for evaluating the expression represented by this tree.
• Figure 12 shows a parse tree for a + (a + d )*(b - c). This tree has more nodes and arcs since it shows the productions used.
• Figure 13 shows the previous parse tree decorated by means of the above translation scheme.

Figure 11: A syntax tree for the expression a + (a + d )*(b - c).

Figure 12: A parse tree for the expression a + (a + d )*(b - c).

Figure 13: A parse tree decorated with translation rules for the expression a + (a + d )*(b - c).