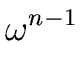Primitive n-th roots of unity of finite fields

Next: Efficient implementation Up: Computing primitive n-th roots of Previous: Some results from group theory

Primitive n-th roots of unity of finite fields

Theorem 6 For n, p > 1, the finite field $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ has a primitive n-th root of unity if and only if n divides p - 1.

Proof. If $\omega$ is a a primitive n-th root of unity in $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ then the set

$\displaystyle \Omega$ = {1, $\displaystyle \omega$ ,..., $\displaystyle \omega^{{{n-1}}}_{{}}$ }

(42)

forms a cyclic subgroup H of the multiplicative group G_p-1 of $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ . By vertue of Lagrange's theorem (Theorem 5) the cardinality of H divides that of G_p-1. Since G_p-1 has p - 1 elements, n divides p - 1.

Conversly, it is known from finite field theory that G_p-1 is a cyclic group (even if p is a power of a prime rather than a prime). Let $\alpha$ be a generator of this group, that is

G_p-1 = {1, $\displaystyle \alpha$ , $\displaystyle \alpha^{{2}}_{{}}$ ,..., $\displaystyle \alpha^{{{p-2}}}_{{}}$ }

(43)

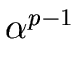Recall that $\alpha^{{{p-1}}}_{{}}$ = 1 from the little Fermat's theorem. Let n > 1 be an integer dividing p - 1 and define

$\displaystyle \omega$ = $\displaystyle \alpha^{{{(p-1)/n}}}_{{}}$ .

(44)

Then we have

$\displaystyle \omega^{{n}}_{{}}$ = 1.

(45)

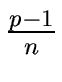For all 0 < k < n we have k ${\frac{{p-1}}{{n}}}$ < p - 1 so we have

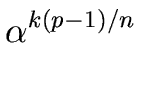$\displaystyle \omega^{{k}}_{{}}$ = $\displaystyle \alpha^{{{k(p-1)/n}}}_{{}}$ $\displaystyle \neq$ 1.

(46)

This shows that $\omega$ is a primitive n-th root of unity. $\qedsymbol$

Example 6 Since 8 | (41 - 1) in $\mbox{${\mathbb Z}$}$ /41 $\mbox{${\mathbb Z}$}$ we have primitive 8-th root of unity. In fact the element 14 $\in$ $\mbox{${\mathbb Z}$}$ /41 $\mbox{${\mathbb Z}$}$ is such a root of unity.

Remark 5 Theorem 6 gives a necessary and sufficient condition for the existence of primitive n-th roots of unity in $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ . But this does not give an algorithm to construct them.

We could use brute force. Given $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ , for every n that we are interested in, for every g $\in$ G_p-1 try if the following both statements hold:

gⁿ = 1,
for every prime divisor t of n we have g^n/t $\neq$ 1.

However we can reduce the complexity of this search by computing a generator of G_p-1 by means of Theorem 7 and then applying Relation (44).

Theorem 7 An element $\alpha$ of the multiplicative subgroup G_p-1 of the prime finite field $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ is a generator of G_p-1 iff for every prime factor t of p - 1 we have

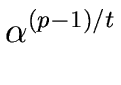$\displaystyle \alpha^{{{(p-1)/t}}}_{{}}$ $\displaystyle \neq$ 1

(47)

Proof. Follows from Lagrange's theorem by using techniques like in the proof of Lemma 1. $\qedsymbol$

Remark 6 For the purpose of multiplying polynomials with coefficients in $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ we are interested in primes p and integers n of the form n = 2^k such that $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ possesses a primitive n-th root of unity. By Theorem 6, the field $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ has such a root if there exists q $\in$ $\mbox{${\mathbb Z}$}$ such that

p = q 2^k + 1

(48)

Such primes are called Fourier primes.

But not all numbers of the form q 2^k + 1 are prime (consider q = k = 2). So how frequent are the primes among the numbers of the form q 2^k + 1 (for a given k). The answer is giving by the following theorem.

Theorem 8 Let a and b be two relatively prime integers. Then the number of primes

in the arithmetic progression a k + b for k = 1, 2,...
and not greater than a given integer x

is approximatively

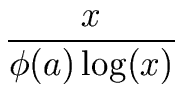$\displaystyle {\frac{{x}}{{{\phi}(a) \, {\log}(x)}}}$

(49)

where $\phi$ (a) is the Euler function at a (the number of integers less than and relatively prime to a).

Remark 7 We apply the previous formula with a = 2^k. All odd numbers less than 2^k are relatively prime to 2^k. (The even numbers are not relatively prime to 2^k.) Thus $\phi$ (2^k) = 2^k-1. Therefore there are approximatively

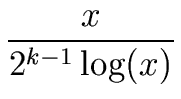$\displaystyle {\frac{{x}}{{2^{k-1} \, {\log}(x)}}}$

(50)

Fourier primes less than a given integer x.

Let x = 2³¹, which represents the usual size required for single precision integers. For k = 20, there are approximatively 130 Fourier primes

of the form 2^e k + 1 with e $\geq$ 20,
and in the range 2^{20 ...}2³¹.

This shows that there are 130 prime finite fields $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ such that

p fits in a machine integer (for a 32-bit processor)
and allowing multiplication of polynomials in $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ [x] whose product is of degree less than 1048576.

So it looks like we have many possible primes for doing fast modular computations with polynomials. However primes p such that p² fits in a machine integer are preferable in order to avoid the use of two machine words for multiplying two elements of $\mbox{${\mathbb Z}$}$ /p $\mbox{${\mathbb Z}$}$ .

In the BasicMath library, one of the parents of libalgebra, nice primes are organized in tables. So there is a category for tables of primes!

macro SI == SingleInteger;

PrimesTableCategory(s: SI): Category ==  with {
        sizeBound: () -> SI;
        tableSize: () -> SI;
        rank: SI -> Partial(SI);
        maxPrime: () -> SI;
        minPrime: () -> SI;
        previousPrime: SI -> SI;
        nextPrime: SI -> SI;
        primes: () -> Generator(SI);
        FourierDegree: SI -> SI;
        getPrimeOfFourierDegree: SI -> SI;
        nextPrimeOfFourierDegree: (SI, SI) -> SI;
        unitsGenerator: SI -> SI;
        primitiveRootofUnity: (SI, SI) -> SI;
}

where

PrimesTableCategory(s) specifies the operations that we expect from a table of primes p less than 2^s. For obvious reasons, this category is restricted to primes that fit in a machine word.
sizeBound() returns s.
tableSize() returns the number of entries in the table.
rank(p) returns tha rank of p in the table if it lies in.
FourierDegree(p) returns the biggest integer r in the table such that 2^r divides p - 1.
getPrimeOfFourierDegree(r) returns the smallest prime p in the table such that FourierDegree(p) >= r, if any, otherwise 0 is returned.
nextPrimeOfFourierDegree(n,r) returns the smallest prime p in the table such that FourierDegree(p) = r and p > n hold, otherwise 0 is returned.
unitsGenerator(p) assuming that p lies in the table returns a generator of the units group of the integers modulo p.
primitiveRootofUnity(p,n) assuming that p lies in the table and assuming 0 < n $\leq$ r where r is FourierDegree(p), returns a primitive 2ⁿ-root of unity of the units group of the integers modulo p.

macro SI == SingleInteger;

FourierPrimesTableCategory(r: SI, s: SI): Category ==  with {
        FourierDegree: () -> SI
        sizeBound: () -> SI
        tableSize: () -> SI
        rank: SI -> Partial(SI)
        maxPrime: () -> SI
        minPrime: () -> SI
        previousPrime: SI -> SI
        nextPrime: SI -> SI
        primes: () -> Generator(SI)
        unitsGenerator: SI -> SI
        primitiveRootofUnity: (SI, SI) -> SI
}

whereFourierPrimesTableCategory(r,s) specifies the operations that we expect from the table of Fourier primes p less than 2^s and such that there exists an odd integer q satisfying p - 1 = 2^rq. Again we restrict to primes that fit in a machine word.

F6P15: FourierPrimesTableCategory(6,15) == add {
         local fd: SI == 6;
         local sb: SI == 15;
 -------------------------------------------------------------------- 
 -- Table (6,15)                                                  -- 
 -------------------------------------------------------------------- 

 -- Maximal size for a FFT: 2^6
 -- Number of 6-Fourier primes less than 2^15 is 58
	MAXINDEX: SingleInteger == 58;
 -- These Fourier primes are: 
	local primeList: Array SingleInteger := 
	   [193, 449, 577, 1217, 1601, 2113, 2753, 3137, 
	    4289, 4673, 4801, 5441, 5569, 5953, 6337, 6977, 
	    7489, 7873, 8513, 8641, 9281, 10177, 10433, 11329, 
	    11969, 12097, 13121, 13249, 13633, 14401, 14657, 15809, 
	    15937, 16193, 17729, 19009, 19777, 20161, 20929, 21313, 
	    21569, 22721, 23873, 24001, 25153, 25409, 25537, 25793, 
	    26177, 26561, 27073, 27329, 27457, 28097, 29633, 29761, 
	    30529, 32321];

 -- The corresponding units generators are: 
	local generatorList: Array SingleInteger := 
	   [5, 3, 5, 3, 3, 5, 3, 3, 
	    3, 3, 7, 3, 13, 7, 10, 3, 
	    7, 5, 5, 17, 3, 7, 3, 7, 
	    3, 5, 7, 7, 5, 11, 3, 3, 
	    7, 5, 3, 23, 11, 13, 7, 5, 
	    3, 3, 3, 14, 10, 3, 10, 3, 
	    3, 3, 5, 3, 7, 3, 3, 17, 
	    13, 6];

        FourierDegree(): SI == fd;
        sizeBound(): SI == sb;
        tableSize(): SI == MAXINDEX;
..............................................        
}

F7P15: FourierPrimesTableCategory(7,15) == add {
         local fd: SI == 7;
         local sb: SI == 15;
 -------------------------------------------------------------------- 
 -- Table (7,15)                                                  -- 
 -------------------------------------------------------------------- 

 -- Maximal size for a FFT: 2^7
 -- Number of 7-Fourier primes less than 2^15 is 29
	MAXINDEX: SingleInteger == 29;
 -- These Fourier primes are: 
	local primeList: Array SingleInteger := 
	   [641, 1153, 1409, 2689, 3457, 4481, 4993, 6529, 
	    7297, 9601, 9857, 10369, 11393, 12161, 13441, 13697, 
	    15233, 16001, 18049, 19073, 19841, 20353, 21121, 21377, 
	    26497, 28289, 29569, 30593, 31873];

 -- The corresponding units generators are: 
	local generatorList: Array SingleInteger := 
	   [3, 5, 3, 19, 7, 3, 5, 7, 
	    5, 13, 5, 13, 3, 3, 11, 3, 
	    3, 3, 13, 3, 3, 5, 19, 3, 
	    5, 6, 17, 3, 11];

        FourierDegree(): SI == fd;
        sizeBound(): SI == sb;
        tableSize(): SI == MAXINDEX;
...........................................................

F8P15: FourierPrimesTableCategory(8,15) == add {
         local fd: SI == 8;
         local sb: SI == 15;
 -------------------------------------------------------------------- 
 -- Table (8,15)                                                  -- 
 -------------------------------------------------------------------- 

 -- Maximal size for a FFT: 2^8
 -- Number of 8-Fourier primes less than 2^15 is 12
	MAXINDEX: SingleInteger == 12;
 -- These Fourier primes are: 
	local primeList: Array SingleInteger := 
	   [257, 769, 3329, 7937, 9473, 14081, 14593, 22273, 
	    23297, 26881, 30977, 31489];

 -- The corresponding units generators are: 
	local generatorList: Array SingleInteger := 
	   [3, 11, 3, 3, 3, 3, 5, 5, 
	    3, 11, 3, 7];

        FourierDegree(): SI == fd;
        sizeBound(): SI == sb;
        tableSize(): SI == MAXINDEX;
...........................................................

9P23: FourierPrimesTableCategory(9,23) == add {
         local fd: SI == 9;
         local sb: SI == 23;
 -------------------------------------------------------------------- 
 -- Table (9,23)                                                  -- 
 -------------------------------------------------------------------- 

 -- Maximal size for a FFT: 2^9
 -- Number of 9-Fourier primes less than 2^23 is 1092
        MAXINDEX: SingleInteger == 1092;
 -- These Fourier primes are: 
        local primeList: Array SingleInteger := 
           [7681, 10753, 11777, 17921, 23041, 26113, 32257,
...........................................................

F10P24: FourierPrimesTableCategory(10,24) == add {
         local fd: SI == 10;
         local sb: SI == 24;
 -------------------------------------------------------------------- 
 -- Table (10,24)                                                  -- 
 -------------------------------------------------------------------- 

 -- Maximal size for a FFT: 2^10
 -- Number of 10-Fourier primes less than 2^24 is 1087
        MAXINDEX: SingleInteger == 1087;
 -- These Fourier primes are: 
        local primeList: Array SingleInteger := 
           [13313, 15361, 19457, 25601,
...........................................................

F11P25: FourierPrimesTableCategory(11,25) == add {
         local fd: SI == 11;
         local sb: SI == 25;
 -------------------------------------------------------------------- 
 -- Table (11,25)                                                  -- 
 -------------------------------------------------------------------- 

 -- Maximal size for a FFT: 2^11
 -- Number of 11-Fourier primes less than 2^25 is 978
        MAXINDEX: SingleInteger == 978;
 -- These Fourier primes are: 
        local primeList: Array SingleInteger := 
           [18433, 
...........................................................

F12P26: FourierPrimesTableCategory(12,26) == add {
         local fd: SI == 12;
         local sb: SI == 26;
 -------------------------------------------------------------------- 
 -- Table (12,26)                                                  -- 
 -------------------------------------------------------------------- 

 -- Maximal size for a FFT: 2^12
 -- Number of 12-Fourier primes less than 2^26 is 972
        MAXINDEX: SingleInteger == 972;
 -- These Fourier primes are: 
        local primeList: Array SingleInteger := 
           [12289,
...........................................................

Next: Efficient implementation Up: Computing primitive n-th roots of Previous: Some results from group theory

Marc Moreno Maza
2003-06-06