

Next: Mignotte's factor bound
Up: Advanced Computer Algebra: The resultant
Previous: The resultant
Let
f, g 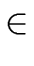 R[x] be nonzero polynomials for an Euclidean domain R.
Let p
R[x] be nonzero polynomials for an Euclidean domain R.
Let p 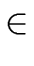 R be a prime.
We denote by
a
R be a prime.
We denote by
a 
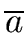 the reduction
modulo p.
We know from the previous section that
the reduction
modulo p.
We know from the previous section that
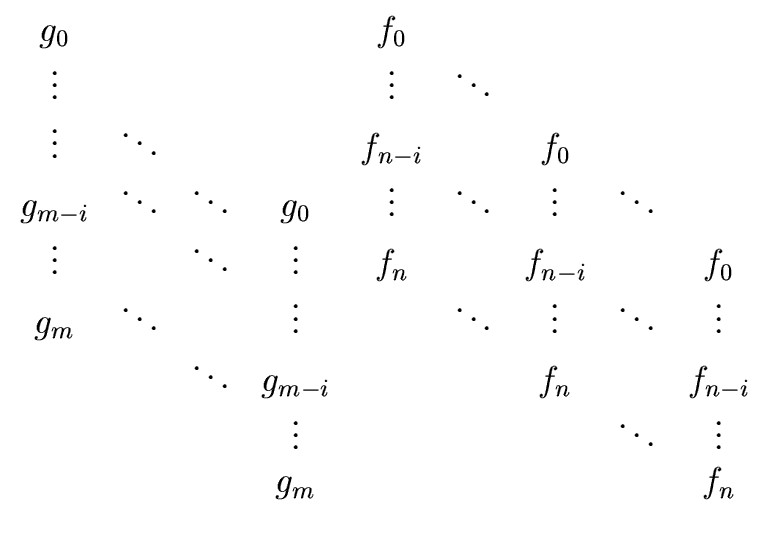
gcd(f, g)  R R  res(f, g) res(f, g)  0 0 |
(36) |
The formula of the resultant of f and g shows that
res(f, g) is a
multivariate polynomial expression in the coefficients of f and g.
Hence we might be tempted to say
-
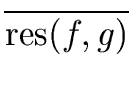 = res(
= res( ,
,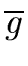 ).
).
-
 and
and
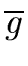 are coprime in R/p[x] iff p does not divide
res(f, g).
are coprime in R/p[x] iff p does not divide
res(f, g).
Example 1
Consider
R = 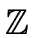 , p = 2, f = x + 2 and g = x.
Then we have
, p = 2, f = x + 2 and g = x.
Then we have
res(f, g) = - 2  0 mod2 and res( 0 mod2 and res(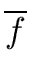 , ,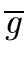 ) = 0 ) = 0 |
(37) |
as expected.
But when
f = 4x3 - x and
g = 2x + 1 we have
res(f, g) = 0 and res(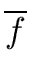 , ,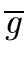 ) = res(x, 1) = 1 ) = res(x, 1) = 1 |
(38) |
The reason for this unexpected behavior in the last example
is that the Sylvester matrix of
 = x and
= x and
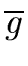 = 1 is
and thus is not the reduction modulo 2 of the
Sylvester matrix of f and g which is
In other words the res
= 1 is
and thus is not the reduction modulo 2 of the
Sylvester matrix of f and g which is
In other words the res operation for

and
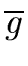
is not
the reduction modulo 2 of the
res operation for
f and
g.
This is because the
res operation depends on the
degrees of its input polynomials.
Fortunately this nuisance disappears when
p does not
divide at least one of the leading coefficients.
Lemma 2
Let
R be a commutative ring with identity element.
Let
f,
g 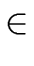 R
R[
x] be nonzero polynomials.
Let
r be their resultant.
Let
I be an ideal if
R and let denote by
a 
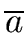
the reduction
modulo
I.
Assume that
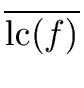 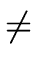 0 0 |
(41) |
Then we have
Moreover, if
R/
I is a UFD, then we have
Proof.
Let us write:
| f = fnxn + ... + f0 and g = gmxm + ... + g0 |
(44) |
with
fn 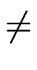
0 and
gm 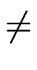
0.
If
n = 0 then
Sylv(
f,
g) and
Sylv(

,
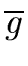
)
are both diagonal with
f on the diagonal.
Then in that case
If
n > 0 we distinguish two cases.
If
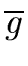
= 0 then
res(

,
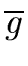
) = 0
(by Definition
4).
Moreover each
g-column of
Sylv(
f,
g) is zero modulo
I such that

= 0 too.
From now on assume
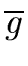
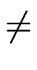
0 and let
i be the smallest index such that
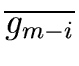
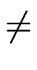
0 holds.
By exchanging the
f-
zone with the
g-
zone we have also
Let
M be the submatrix obtained from
Sylv(
g,
f ) by deleting the
last
i rows and the last
i columns.
Observe that we have
Since
we obtain
This shows that we have
and the first claim of the lemma is proved.
The second claim follows from
Proposition
6.

Theorem 3
Let
f,
g 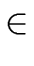 R
R[
x] be nonzero polynomials for an Euclidean Domain
R.
Let
p 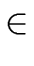 R
R be a prime.
Let
h = gcd(f, g), e = deg(h). and 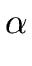 = lc(h) = lc(h) |
(52) |
Assume that
p does not divide
| b = gcd(lc(f ), lc(g)) |
(53) |
Finally let
e * = deg(gcd(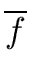 , ,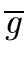 )) )) |
(54) |
Then we have
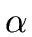 divides b
divides b
-
e *
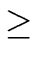 e
e
-
e * = e
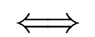
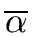 gcd(
gcd( ,
,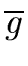 ) =
) = 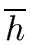
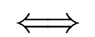 p
p 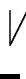 res(f /h, g/h)
res(f /h, g/h)
Proof.
Since in
R[
x]
we have in
R
| lc(h) | lc(f ) and lc(h) | lc(g). |
(56) |
Therefore
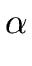 = lc(h) | gcd(lc(f ), lc(g)) = b = lc(h) | gcd(lc(f ), lc(g)) = b |
(57) |
and the first claim is proved.
Consider now the cofactors of
f and
g in
R[
x]
| u = f /h and v = g/h. |
(58) |
Then we have
which shows that
and implies that
Since
p does not divide
b, it cannot not divide
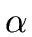
neither.
Hence the leading coefficient of
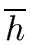
is
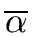
and we have
deg(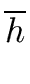 ) = deg(h) ) = deg(h) |
(62) |
Therefore
e = deg(h) 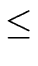 deg(gcd( deg(gcd(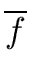 , ,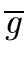 )) = e * )) = e * |
(63) |
and the second claim is proved.
Now consider the case where
e = e * .
Since
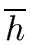 divides
gcd(
divides
gcd( ,
,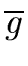 )
and since
gcd(
)
and since
gcd( ,
,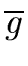 ) is monic (as a gcd over
the field R/p) there exists a unit
) is monic (as a gcd over
the field R/p) there exists a unit 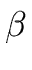 such that
such that
Since the leading coefficient of
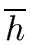
is
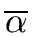
we have in fact
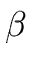 = = 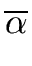 |
(65) |
Therefore we have the following equivalence
It remains to prove that
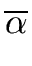 gcd( gcd(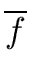 , ,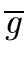 ) = ) = 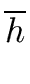  p p  res(f /h, g/h) res(f /h, g/h) |
(67) |
Observe that
p cannot divide both
lc(
u) and
lc(
v).
If this was the case
then from Relation (
59) (and since
p does not divide
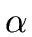
=
lc(
h))
p would divide
lc(
f ) and
lc(
g), and thus
b.
A contradiction. Therefore we can assume that
p does not divide
lc(
u).
By applying Lemma
2 we obtain
By applying Proposition
5
this leads to
p | res(u, v)  gcd( gcd(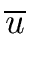 , , ) ) 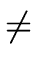 1 1 |
(69) |
From Relation (
59) we have
Therefore
p  res(u, v) res(u, v)  gcd( gcd(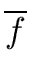 , ,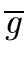 ) = 1 × ) = 1 × 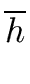 / /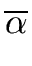 |
(71) |
This concludes the proof of the theorem.

Definition 5
Let
f,
g 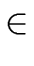 R
R[
x] be nonzero polynomials for an Euclidean domain
R.
Let
h 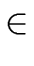 R
R[
x] be
gcd(
f,
g).
A prime element
p 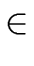 R
R is said
lucky if
p does not divide
res(
f /
h,
g/
h) otherwise it is said
unlucky.
Example 2
Consider
f = 12x3 - 28x2 + 20x - 4,
g = - 12x2 + 10x - 2
and p = 17.
We have the following computation in AXIOM (where we do not display types)
N := NonNegativeInteger
(1) NonNegativeInteger
Z := Integer
(2) Integer
U := UnivariatePolynomial(x,Z)
(3) UnivariatePolynomial(x,Integer)
f: U := 12*x^3 -28*x^2 +20*x - 4
3 2
(4) 12x - 28x + 20x - 4
g: U := -12*x^2 +10*x -2
2
(5) - 12x + 10x - 2
resultant(f,g)
(6) 0
h: U := gcd(f,g)
(7) 6x - 2
r: Z := resultant(exquo(f,h),exquo(g,h))
(8) 2
K17 := PrimeField(17)
(9) PrimeField 17
r :: K17
(10) 2
U17 := UnivariatePolynomial(x,K17)
(11) UnivariatePolynomial(x,PrimeField 17)
f17: U17 := f :: U17
3 2
(12) 12x + 6x + 3x + 13
g17: U17 := g :: U17
2
(13) 5x + 10x + 15
h17: U17 := h ::U17
(14) 6x + 15
c17 := gcd(f17,g17)
(15) x + 11
h17 - (leadingCoefficient(h17)) * c17
(16) 0
Example 3
Consider
f = x4 - 3x2 + 2x,
g = x3 - 1
and p = 13.
We have the following computation in AXIOM (where we do not display types)
The variables N, Z, U are defined as above.
f: U := x^4 -3*x^3 + 2*x
4 3
(4) x - 3x + 2x
g: U := x^3 -1
3
(5) x - 1
resultant(f,g)
(6) 0
h: U := gcd(f,g)
(7) x - 1
r: Z := resultant(exquo(f,h),exquo(g,h))
(8) 9
K3 := PrimeField(3)
(9) PrimeField 3
r :: K3
(10) 0
U3 := UnivariatePolynomial(x,K3)
(11) UnivariatePolynomial(x,PrimeField 3)
f3: U3 := f :: U3
4
(12) x + 2x
g3: U3 := g :: U3
3
(13) x + 2
h3: U3 := h ::U3
(14) x + 2
c3 := gcd(f3,g3)
3
(15) x + 2
exquo(c3, h3)
2
(16) x + x + 1


Next: Mignotte's factor bound
Up: Advanced Computer Algebra: The resultant
Previous: The resultant
Marc Moreno Maza
2004-04-27
![]() R[x] be nonzero polynomials for an Euclidean domain R.
Let p
R[x] be nonzero polynomials for an Euclidean domain R.
Let p ![]() R be a prime.
We denote by
a
R be a prime.
We denote by
a ![]()
![]() the reduction
modulo p.
We know from the previous section that
the reduction
modulo p.
We know from the previous section that
 res(f, g)
res(f, g) 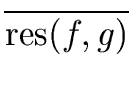 = res(
= res(
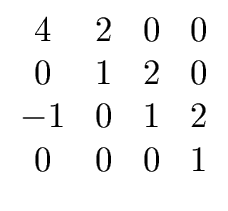
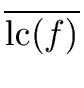
 res(
res( deg(gcd(
deg(gcd( =
= 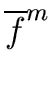 = res(
= res(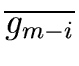

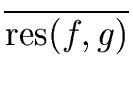 = (- 1)nm
= (- 1)nm 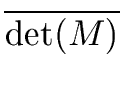
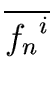
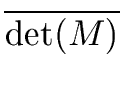 = det(
= det(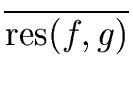 = (- 1)nm res(
= (- 1)nm res(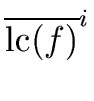
 res(
res(![]() divides
gcd(
divides
gcd(![]() ,
,![]() )
and since
gcd(
)
and since
gcd(![]() ,
,![]() ) is monic (as a gcd over
the field R/p) there exists a unit
) is monic (as a gcd over
the field R/p) there exists a unit ![]() such that
such that

 p
p 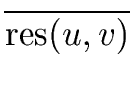 = 0
= 0  res(
res( gcd(
gcd( gcd(
gcd(